Question

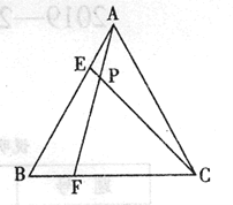
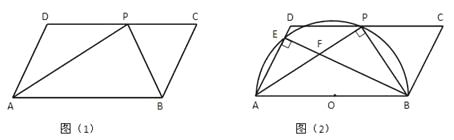
【题目】如图（1），在□ABCD中，P是CD边上的一点，AP与BP分别平分∠DAB和∠CBA。

【1】判断△APB是什么三角形？证明你的结论；

【2】比较DP与PC的大小；

【3】如图（2）以AB为直径作半圆O，交AD于点E，连结BE与AP交于点F，若AD=5cm，AP=8cm，求证△AEF∽△APB，并求tan∠AFE的值。

Answer 1

【答案】

【1】 △APB是直角三角形，理由如下：

∵在□ABCD中，AD∥BC，

∴∠DAB +∠ABC = 180°；

又∵AP与BP分别平分∠DAB和∠CBA，

∴∠PAB =，∠PBA =，

∴∠PAB+∠PBA=，

∴△APB是直角三角形；

【2】 ∵DC∥AB，

∴∠BAP =∠DPA．

∵∠DAP =∠PAB，

∴∠DAP =∠DPA，

∴DA = DP

同理证得CP=CB．

∴DP = PC

【3】 ∵AB是⊙O直径，

∴∠AEB = 90°．

又（1）易知∠APB = 90°．

∴∠AEB =∠APB，

∵AP为角平分线，即∠EAF=∠PAB，

∴△AEF∽△APB，

由（2）可知DP =" PC" = AD，

∴ AB =" DC" =" 2AD" = 10cm，

在Rt△PAB中，（cm）

又△AEF∽△APB，

得∠AFE=∠ABP，

∴tan∠AFE = tan∠ABP=。

【解析】

【1】可通过角的度数来判断三角形APB的形状．由于ABCD是平行四边形，AD∥BC，那么同旁内角∠DAB和∠CBA的和应该是180°，AP，BE平分∠DAB，∠ABP，于是∠PAB和∠ABP的和就应该是90°，即∠APB=90°，因此可得出三角形APB的形状．

【2】可通过平行和角平分线，通过等角对等边得出DP=AP，同理可证出PC=BC，根据平行四边形的性质，AD=BC，可得出DP=PC．

【3】利用两个角相等求出△AEF∽△APB，然后利用（2）求出PB的长度，在根据∠AFE=∠ABP，然后求出tan∠AFE的值.