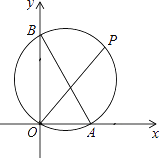题目内容
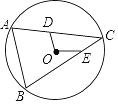
【题目】如图,点C是⊙O上一点,⊙O的半径为![]() ,D、E分别是弦AC、BC上一动点,且OD=OE=
,D、E分别是弦AC、BC上一动点,且OD=OE=![]() ,则AB的最大值为( )
,则AB的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
先判断出OD⊥AC、OE⊥BC时∠ACB最大,从而得到AB最大,连接OC,根据直角三角形30°角所对的直角边等于斜边的一半求出∠ACO=30°,再根据垂径定理和勾股定理求出AC,然后求出∠ACB=60°,再求出AC=BC,从而得到△ABC是等边三角形,最后根据等边三角形的性质可得AB=AC.
:
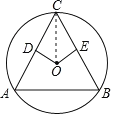
如图,当OD⊥AC、OE⊥BC时∠ACB最大,AB最大,
连接OC,
∵O的半径为2![]() ,OD=
,OD=![]() ,
,
∴∠ACO=30°,
∴AC=2CD=2![]() =2
=2![]() =2
=2![]() ,
,
同理可得∠BOC=30°,
∴∠ACB=60°,
∵OD=OE,OD⊥AC、OE⊥BC,∴AC=BC,
∴△ABC是等边三角形,
∴AB=AC=2![]() ,
,
即AB的最大值为2![]() .
.
故答案选A.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目