Question

【题目】中，，的顶点是底边的中点，两边分别与交于点．

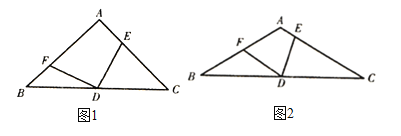
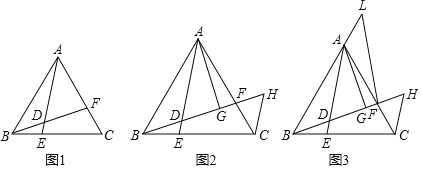
（1）如图1， ，当的位置变化时，是否随之变化？证明你的结论；

（2）如图2，当，当 °时，（1）中的结论仍然成立，求出此时的值．

Answer 1

【答案】（1）BF+CE＝a，是定值，不变．见解析；（2）60，9

【解析】

（1）结论：BF＋CE=a，是定值．如图1中，连接AD．只要证明△BDF≌△ADE即可解决问题；
（2）当∠EDF=60°时，BF＋EC=9，是定值．连接AD，作DM⊥AB于M，DN⊥AC于N．只要证明△DMF≌△DNE（ASA），推出FM=EN，由含30°的直角三角形的性质，推出BM=CN=，推出BF＋CE=BMFM＋CN＋EN=2BM，即可解决问题．

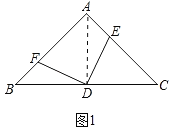
解：（1）结论：BF+CE=a，是定值．

理由：如图1中，连接AD．

∵AB=AC，∠BAC=90°，BD=CD，

∴AD⊥BC，∠B=∠C=∠BAD=∠CAD=45°，AD=BD=CD．

∵∠EDF=∠ADB=90°，

∴∠BDF=∠ADE，

∴△BDF≌△ADE（ASA），

∴BF=AE，

∴BF+CE=AE+CE=AC=a，是定值．

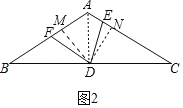
（2）当∠EDF=60°时，BF+EC=9，是定值．

理由：如图2中，连接AD，作DM⊥AB于M，DN⊥AC于N．

∵∠AMD=∠AND=90°，∠A=120°，

∴∠MDN=∠EDF=60°，

∴∠MDF=∠NDE，

∵AB=AC，BD=CD，

∴∠BAD=∠CAD，

∵DM⊥AB于M，DN⊥AC于N，

∴DM=DN，

∴△DMF≌△DNE（ASA），

∴FM=EN，

∵AB=AC，BD=CD，

∴AD⊥BC．

∵∠B=∠C=30°，

∴AD=AB=AC=3，∠BAD=∠CAD=60°．

又∵DM⊥AB，DN⊥AC，

∴∠ADM=∠ADN=30°，

∴AM=AN=AD=，

∴BM=CN=，

∴BF+CE=BM﹣FM+CN+EN=2BM=9，是定值．