题目内容
【题目】如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan ∠BDE=

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
连接AD,由△ABC中,AB=AC=13,BC=10,D为BC中点,利用等腰三角形三线合一的性质,可证得AD⊥BC,再利用勾股定理,求得AD的长,那么在直角△ABD中根据三角函数的定义求出tan∠BAD,然后根据同角的余角相等得出∠BDE=∠BAD,于是tan∠BDE=tan∠BAD.
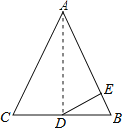
连接AD,
∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BD=![]() BC=5,
BC=5,
∴![]() ,
,
∴![]() .
.
∵AD⊥BC,DE⊥AB,
∴∠BDE+∠ADE=90°,∠BAD+∠ADE=90°,
∴∠BDE=∠BAD,
∴tan∠BDE=tan∠BAD= ![]() .
.
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目