��Ŀ����
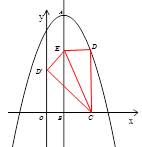
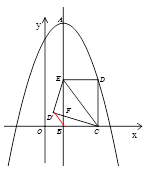
��ͼ����ƽ��ֱ������ϵ�У�������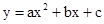 �Ķ���A������Ϊ��3,15�����ҹ��㣨��2��10�����Գ���AB��
�Ķ���A������Ϊ��3,15�����ҹ��㣨��2��10�����Գ���AB�� ���ڵ�B����E���߶�AB��һ���㣬��EBΪ���ڶԳ����Ҳ�������EBCD��ʹ�õ�Dǡ�������������ϣ���D���ǵ�D����ֱ��EC����ԳƵ�.
���ڵ�B����E���߶�AB��һ���㣬��EBΪ���ڶԳ����Ҳ�������EBCD��ʹ�õ�Dǡ�������������ϣ���D���ǵ�D����ֱ��EC����ԳƵ�.
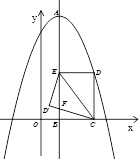
��1���������ߵĽ���ʽ��
��2������D��ǡ������ ���ϵĵ㣨0��6��ʱ�����ʱD������ꣻ
���ϵĵ㣨0��6��ʱ�����ʱD������ꣻ
��3��ֱ��CD�佻�Գ���AB�ڵ�F,
�ٵ���D���ڶԳ���AB�����ʱ���ҡ�ED��F�ס�CDE�����DE:DC��ֵ��
������B D�䣬�Ƿ���ڵ�E��ʹ��E D��BΪ���������Σ������ڣ���ֱ��д��BE:BC��ֵ������������˵������.
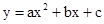 �Ķ���A������Ϊ��3,15�����ҹ��㣨��2��10�����Գ���AB��
�Ķ���A������Ϊ��3,15�����ҹ��㣨��2��10�����Գ���AB�� ���ڵ�B����E���߶�AB��һ���㣬��EBΪ���ڶԳ����Ҳ�������EBCD��ʹ�õ�Dǡ�������������ϣ���D���ǵ�D����ֱ��EC����ԳƵ�.
���ڵ�B����E���߶�AB��һ���㣬��EBΪ���ڶԳ����Ҳ�������EBCD��ʹ�õ�Dǡ�������������ϣ���D���ǵ�D����ֱ��EC����ԳƵ�.
��1���������ߵĽ���ʽ��
��2������D��ǡ������
 ���ϵĵ㣨0��6��ʱ�����ʱD������ꣻ
���ϵĵ㣨0��6��ʱ�����ʱD������ꣻ��3��ֱ��CD�佻�Գ���AB�ڵ�F,
�ٵ���D���ڶԳ���AB�����ʱ���ҡ�ED��F�ס�CDE�����DE:DC��ֵ��
������B D�䣬�Ƿ���ڵ�E��ʹ��E D��BΪ���������Σ������ڣ���ֱ��д��BE:BC��ֵ������������˵������.
��1��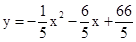 ;��2��(8,10); ��3����
;��2��(8,10); ��3����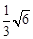 ;��
;��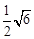 .
.
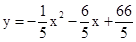 ;��2��(8,10); ��3����
;��2��(8,10); ��3����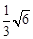 ;��
;��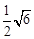 .
.�����������1������֪,Ӧ�ô���ϵ�����趥��ʽ���;
��2�����ݹ��ɶ�������ԳƵ������з��������;
��3�����ɹ��ɶ��������������ε�������ʽ���;
���ɢٿ�֪��ED��F�ա�CBFʱ, D��F=BF,�Ӷ��ó�����.
�����������1����������
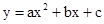 �Ķ���A������Ϊ��3,15����
�Ķ���A������Ϊ��3,15��������������ߵĽ���ʽΪ
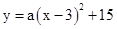 .
.�������߹��㣨��2��10��, ��
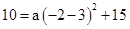 .���
.���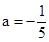 .
.�������ߵĽ���ʽΪ
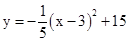 ,��
,��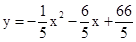 .
.��2����D(x,��),��E(3, ��), DE="x-3," DC=��.
��D�䣨0��6��,���ݹ��ɶ���,��: D��C=
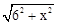 , D��E=
, D��E=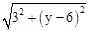 ,
,������ԳƵ�����,��D��C="DC," D��E= DE,��
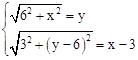 ,���
,��� .
.���ʱD�������Ϊ(8,10).
��3������֤��ED��F�ա�CBF,��D��F=BF.
��D��C=DC=a,D��E=DE=b,D��F=BF=c,
��Rt��CBF��,�ɹ��ɶ���,��:CF2=BF2+D��C2,��(D��C- D��F)2=BF2+D��C2.
��
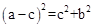 ,����,��
,����,��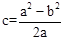 .
.�ߡ�ED��F�ס�CDE����
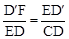 ,��
,��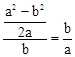 ,��
,��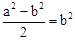 ,��
,��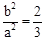 ,��
,��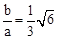 .
.��DE:DC=
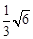 .
.�ڴ���,�ɢٿ�֪BE:BC=
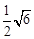 .
.

��ϰ��ϵ�д�
�����Ŀ
 ������A(4,0),B(2,2),����OB,AB��
������A(4,0),B(2,2),����OB,AB��
 ��
��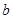 ��ֵ��
��ֵ�� ��ö��κ�������A,B����,����A�㣨3,4��,B����y����.
��ö��κ�������A,B����,����A�㣨3,4��,B����y����.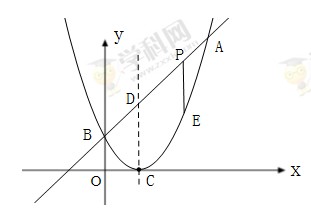
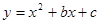 ���㣨2��-2���ͣ�-1��10������x�ύ��A��B���㣬��y�ύ��C�㣮
���㣨2��-2���ͣ�-1��10������x�ύ��A��B���㣬��y�ύ��C�㣮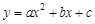 ��ͼ����x�ύ�ڵ�A��-1, 0������y�ύ�ڵ�C��0��-5�����Ҿ�����D��3��-8��.
��ͼ����x�ύ�ڵ�A��-1, 0������y�ύ�ڵ�C��0��-5�����Ҿ�����D��3��-8��.
 ���������������ε�����ĺ�S����
���������������ε�����ĺ�S����

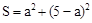
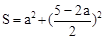
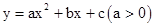 �ĶԳ�����ֱ��x=1���Ҿ�����P����
�ĶԳ�����ֱ��x=1���Ҿ�����P���� ��ֵΪ�� ��
��ֵΪ�� ��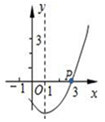
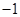
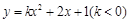 ��ͼ������ǣ� ��
��ͼ������ǣ� ��