题目内容
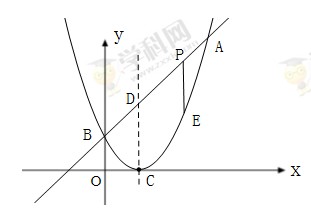
已知二次函数图象顶点为C(1,0),直线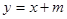 与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.
与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.
(1)求此二次函数的解析式;
(2)P为线段AB上一动点(不与A,B重合),过点P作y轴的平行线与二次函数交于点E.设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式;
(3)D为线段AB与二次函数对称轴的交点,在AB上是否存在一点P,使四边形DCEP为平行四边形?若存在,请求出P点坐标;若不存在,请说明理由.
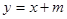 与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.
与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.
(1)求此二次函数的解析式;
(2)P为线段AB上一动点(不与A,B重合),过点P作y轴的平行线与二次函数交于点E.设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式;
(3)D为线段AB与二次函数对称轴的交点,在AB上是否存在一点P,使四边形DCEP为平行四边形?若存在,请求出P点坐标;若不存在,请说明理由.
(1)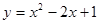 ;(2)
;(2)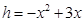 ;(3)存在,P点坐标为(2,3).
;(3)存在,P点坐标为(2,3).
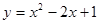 ;(2)
;(2)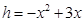 ;(3)存在,P点坐标为(2,3).
;(3)存在,P点坐标为(2,3).试题分析:(1)因为直线y=x+m过点A,将A点坐标直接代入解析式即可求得m的值;设出二次函数的顶点式,将(3,4)代入即可;
(2)由于P和E的横坐标相同,将P点横坐标代入直线和抛物线解析式,可得其纵坐标表达式;
(3)先假设存在点P,根据四边形DCEP是平行四形的条件进行推理,若能求出P点坐标,则证明存在点P,否则P点不存在.
试题解析:(1)把A(3,4)代入
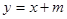
得m=1,
∴
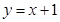 ,
,∴B(0,1),
设二次函数解析式为
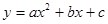 ,
,把A.B.C三点坐标代入得

解得
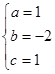
∴
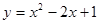 ;
;(2)∵P点在直线
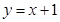 的图象上,
的图象上,∴P点坐标为(
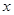 ,
,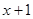 ),
),∵E点在抛物线
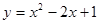 的图象上,
的图象上,∴E点坐标为(
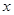 ,
,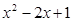 ),
),∴
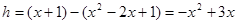 ;
;(3)存在.
易求D点坐标为(1,2),则DC="2" ,
当PE=2时,PE∥DC,四边形DCEP为平行四边形,
即
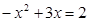 解得
解得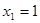 ,
,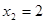 ,
,当
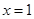 时,PE与DC重合,
时,PE与DC重合,当
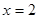 时,代入
时,代入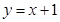 ,
,
∴ P点坐标为(2,3).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

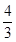 x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少? 分别与y轴、x轴相交于A、B两点,与二次函数
分别与y轴、x轴相交于A、B两点,与二次函数 的图像交于A、C两点.
的图像交于A、C两点.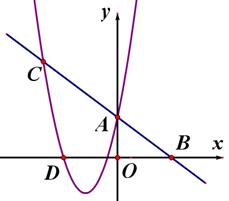
 ,
,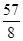 )时,求直线AB的解析式;
)时,求直线AB的解析式;  (k为正整数).
(k为正整数).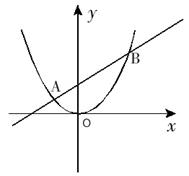
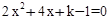 (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数
(k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数 的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交
的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交 轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
 轴上的点(0,6)时,求此时D点的坐标;
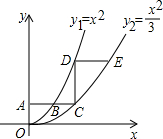
轴上的点(0,6)时,求此时D点的坐标; (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= .
 的对称轴为
的对称轴为 ,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为 .
,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为 .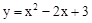 的最小值是( )
的最小值是( )