题目内容
抛物线 经过点A(4,0),B(2,2),连结OB,AB.
经过点A(4,0),B(2,2),连结OB,AB.

(1)求 、
、 的值;
的值;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转l35°得到△OA′B′,写出A′B′的中点P的出标.试判断点P是否在此抛物线上,并说明理由.
 经过点A(4,0),B(2,2),连结OB,AB.
经过点A(4,0),B(2,2),连结OB,AB.
(1)求
 、
、 的值;
的值;(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转l35°得到△OA′B′,写出A′B′的中点P的出标.试判断点P是否在此抛物线上,并说明理由.
(1)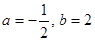 ;(2)证明见解析;(3)点
;(2)证明见解析;(3)点 不在抛物线上.
不在抛物线上.
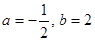 ;(2)证明见解析;(3)点
;(2)证明见解析;(3)点 不在抛物线上.
不在抛物线上.试题分析:(1)将A、B的坐标代入抛物线的解析式中,通过联立方程组即可求出抛物线的解析式;
(2)过B作BC⊥x轴于C,根据A、B的坐标易求得OC=BC=AC=2,由此可证得∠BOC、∠BAC、∠OBC、∠ABC都是45°,即可证得△OAB是等腰直角三角形;
(3)当△OAB绕点O按顺时针方向旋转135°时,OB′正好落在y轴上,易求得OB、AB的长,即可得到OB′、A′B′的长,从而可得到A′、B′的坐标,进而可得到A′B′的中点P点的坐标,然后代入抛物线中进行验证即可.
试题解析:⑴ 由题意,得:
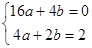 ,
,解得:
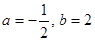 ;
;⑵ 过点
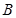 作
作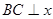 轴于点
轴于点 ,则
,则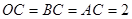 ,
,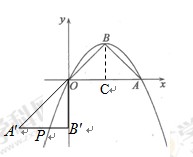
∴
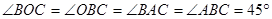 ,
,∴
 ,
,∴
 是等腰直角三角形;
是等腰直角三角形;⑶∵
 是等腰直角三角形,
是等腰直角三角形,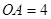 ,
,∴
 ,
,由题意,得:点
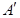 坐标为
坐标为 ,
,∴
 的中点
的中点 的坐标为
的坐标为 ,
,当
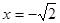 时,
时,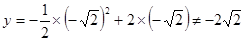
∴点
 不在抛物线上.
不在抛物线上.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少? 轴建立直角坐标系,桥洞上沿形状恰好是抛物线
轴建立直角坐标系,桥洞上沿形状恰好是抛物线 的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.
的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.

 的对称轴是( )
的对称轴是( )



 分别与y轴、x轴相交于A、B两点,与二次函数
分别与y轴、x轴相交于A、B两点,与二次函数 的图像交于A、C两点.
的图像交于A、C两点.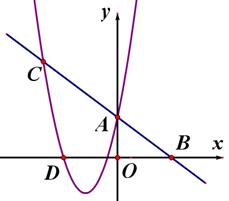
 ,
,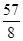 )时,求直线AB的解析式;
)时,求直线AB的解析式;  的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交
的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交 轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
 轴上的点(0,6)时,求此时D点的坐标;
轴上的点(0,6)时,求此时D点的坐标; +bx+c的图像如图所示,则不等式ax
+bx+c的图像如图所示,则不等式ax
 或
或 .其中正确的是( )
.其中正确的是( )
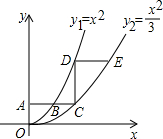
 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= .