Question

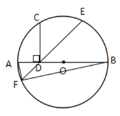
【题目】如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E，连接AD，BC，CO

（1）当∠BCO＝25°时，求∠A的度数；

（2）若CD＝4，BE＝4，求⊙O的半径．

Answer 1

【答案】（1）65°；（2）3.

【解析】

（1）利用圆周角定理即可求解；（2）利用垂径定理求出CE的长，设⊙O的半径为r，则OC＝r，OE＝BE﹣BO＝4﹣r，根据勾股定理即可列出方程求出r.

解：（1）∵OC＝OB，

∴∠BCO＝∠B，

∵∠B＝∠D，

∴∠D＝∠BCO＝25°，

∵CD⊥AB，

∴在Rt△ADE中，∠A＝90°﹣∠D＝90°﹣25°＝65°；

（2）∵AB是⊙O的直径，且CD⊥AB于点E，

∴CE＝CD＝，

在Rt△OCE中，OC2＝CE2+OE2，

设⊙O的半径为r，则OC＝r，OE＝BE﹣BO＝4﹣r，

∴，

解得：r＝3，

∴⊙O的半径为3．