题目内容
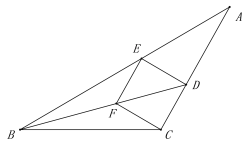
【题目】如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上一点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形.
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长。

【答案】(1)详见解析;(2)当∠ACB=120度时,四边形CDEF是正方形,证明见解析,此时正方形的边长为![]() .
.
【解析】
(1)先证△CBD≌△EBD,由全等三角形的性质得DE=DC,∠BDC=∠BDE,同理△BCF≌△BEF,EF=CF,再根据平行线的性质得∠CFD=∠BDE,等量代换得CFD=∠BDC,可得CF=CD,根据四边相等的四边形是菱形可得结论;
(2)当∠ACB=120度时,四边形CDEF是正方形.由等腰三角形的性质可得∠A=∠ABC=30°,由角平分线得∠CBD=∠EBD=15°,根据平行线的性质得∠BEF=∠A=30°,再由三角形外角的性质可得∠EFD=∠EBD+∠BEF=45°,由菱形的性质可证出∠EFD=∠EDF=45°,则∠FED=90°,菱形CDEF是正方形;设正方形CDEF的边长为x,在Rt△ADE中,利用30°角的直角三角形的性质表示出AD=![]() x,由AB=AC=6可得AD=6-x,则6-x =
x,由AB=AC=6可得AD=6-x,则6-x =![]() x,解方程即可求得正方形的边长.
x,解方程即可求得正方形的边长.
(1)证明:∵BD平分∠ABC
∴∠CBD=∠EBD,
在△CBD和△EBD中
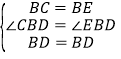 ∴△CBD≌△EBD(SAS)
∴△CBD≌△EBD(SAS)
∴DE=DC,∠BDC=∠BDE
同理△BCF≌△BEF
∴EF=CF
∵CF∥ED ∴∠CFD=∠BDE
∴∠CFD=∠BDC
∴CF=CD
∴EF=CF=CD=DE
∴四边形CDEF是菱形
(2)当∠ACB= 120 度时,四边形CDEF是正方形
证明:∵AC=BC ∠ACB= 120°
∴∠A=∠ABC=30°
∵BD平分∠ABC
∴∠CBD=∠EBD=15°
∵四边形CDEF是菱形
∴EF∥AC
∴∠BEF=∠A=30°
∴∠EFD=∠EBD+∠BEF=15°+30°=45°,
∵EF=ED
∴∠EFD=∠EDF=45°
∴∠FED=90°
∴菱形CDEF是正方形.
设正方形CDEF的边长为x,
在Rt△ADE中,∠A=30° ∴AE=2x, AD=![]() ,
,
∵AD+CD=AC=6
∴![]() +x=6 ∴x=
+x=6 ∴x=![]()
∴正方形CDEF的边长为![]() .
.
故答案为:(1)详见解析;(2)当∠ACB=120度时,四边形CDEF是正方形,证明见解析,此时正方形的边长为![]() .
.






