题目内容
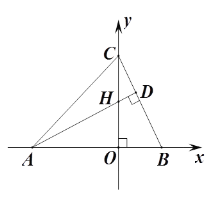
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)答案见解析;(2)2.
【解析】
(1)连接OC,由AB是⊙O的直径可得出∠ACB=90°,即∠ACO+∠OCB=90°,由等腰三角形的性质结合∠BCD=∠A,即可得出∠OCD=90°,即CD是⊙O的切线;
(2)在Rt△OCD中,由勾股定理可求出OD的值,进而可得出BD的长.
(1)连接OC.
∵AB是⊙O的直径,C是⊙O上一点,∴∠ACB=90°,即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,∴∠ACO=∠A=∠BCD,∴∠BCD+∠OCB=90°,即∠OCD=90°,∴CD是⊙O的切线.
(2)在Rt△OCD中,∠OCD=90°,OC=3,CD=4,∴OD=![]() =5,∴BD=OD﹣OB=5﹣3=2.
=5,∴BD=OD﹣OB=5﹣3=2.

练习册系列答案
相关题目