Question

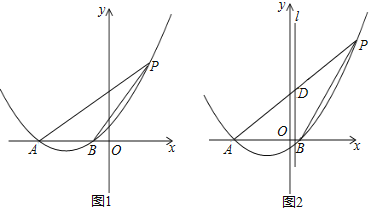
【题目】已知抛物线，其中，直线l是它的对称轴，把该抛物线沿着x轴水平向左平移个单位长度后，与x轴交于点A、B，在B的左侧，如图1，P为平移后的抛物线上位于第一象限内的一点

点A的坐标为______；

若点P的横坐标为，求出当m为何值时的面积最大，并求出这个最大值；

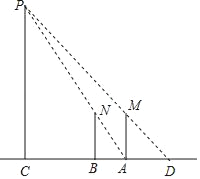
如图2，AP交l于点D，当D为AP的中点时，求证：．

Answer 1

【答案】（1）；（2）；；

【解析】

（1）设y=0，可求平移前抛物线与x轴的交点坐标，即可求平移后点A坐标；

（2）由题意可求平移后抛物线解析式，即可求点P坐标，由三角形面积公式可求S△ABP（m+1）（4﹣m）（m）2，由二次函数的性质可求解；

（3）过点D作DM⊥AB于M，过点P作PN⊥AB于点N，由题意可求点N坐标，即可求AN=PN=m+6，可证∠PAB=45°．

（1）设y=0，则0（x+1）（x﹣m），∴x1=﹣1，x2=m，∴抛物线y（x+1）（x﹣m）与x轴交点坐标（﹣1，0），（m，0）

∵该抛物线沿着x轴水平向左平移个单位长度后，与x轴交于点A、B，∴点A（，0）

故答案为：（，0）．

（2）∵平移后解析式为：y（x+1）（x﹣m（x）（x﹣m），∴当x时，y=4﹣m，∴S△ABP（m+1）（4﹣m）（m）2

∴当m时，△ABP的面积最大值为；

（3）如图，过点D作DM⊥AB于M，过点P作PN⊥AB于点N，∴DM∥PN，∴，且AD=DP，∴MN=AM．

∵点M坐标（，0），点A（，0），∴点N（m，0），∴AN=6+m．

当x=m，y= =m+6，∴PN=m+6=AN，∴∠PAB=45°．