题目内容
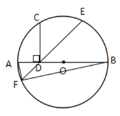
【题目】如图,AB是![]() 的直径,点D是半径OA的中点,过点D作CD⊥AB,交
的直径,点D是半径OA的中点,过点D作CD⊥AB,交![]() 于点C,点E为弧BC的中点,连结ED并延长ED交
于点C,点E为弧BC的中点,连结ED并延长ED交![]() 于点F,连结AF、BF,则( )
于点F,连结AF、BF,则( )
A. sin∠AFE=![]() B. cos∠BFE=
B. cos∠BFE=![]() C. tan∠EDB=
C. tan∠EDB=![]() D. tan∠BAF=
D. tan∠BAF=![]()
【答案】C
【解析】
连接OC,OE,过E作EH⊥AB于H,根据OC=2OD可得∠COD=60°,则∠BOC=120°,由E为弧BC的中点,得∠BOE=60°,则∠BFE=30°,进而可得∠AFE=90°﹣∠BFE=60°,再求出对应的三角形函数值,然后根据CD=![]() OD,可得
OD,可得![]() 的值,进而到tan∠EDB的值
的值,进而到tan∠EDB的值
解:如图,连接OC,OE,过E作EH⊥AB于H,
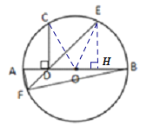
∵点D是半径OA的中点,CD⊥AB,
∴∠COD=60°,即∠BOC=120°,
∴CD=![]() OD,
OD,
∵E为弧BC的中点,
∴∠BOE=60°,EH=CD,H为半径OB的中点,
∴∠BFE=30°,则cos∠BFE=![]() ;
;
又∵AB为直径,
∴∠AFB=90°,
∴∠AFE=90°﹣∠BFE=60°,则sin∠AFE=![]() ;
;
∵EH=CD,
∴tan∠EDB=![]() .
.
故选C.

练习册系列答案
相关题目