题目内容
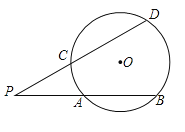
【题目】我们知道：顶点在圆上，并且两边都和圆相交的角叫做圆周角，一条弧所对的圆周角的度数等于它所对的圆心角度数的一半．类似地，我们定义：顶点在圆外，并且两边都和圆相交的角叫做圆外角．
（1）判断：图中有没有圆外角？如果有，请用字母表示出来．
（2）运用所学的数学知识，探究：圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系？将你的发现，用文字表述出来，并说明理由．
【答案】（1）有，
；（2）圆外角的度数等于它所夹的弧所对的圆心角的度数的差的一半，见解析
【解析】
（1）由于∠DPB的两边与圆相交，所以∠DPB是圆外角．
（2）连接DA，OA，OB，OC，OD，根据圆周角定理及外角定理进行分析即可．
解：
是圆外角．
圆外角的度数等于它所夹的弧所对的圆心角的度数的差的一半．
理由如下：连结
，
．
练习册系列答案
相关题目
