题目内容
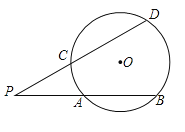
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上一点,以点
上一点,以点![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的半径和
的半径和![]() 的长.
的长.
【答案】(1)见解析;(2)![]() 的半径是6,
的半径是6,![]() 的长是
的长是![]() .
.
【解析】
(1)利用切线的性质证得OD=OC,证得BO为![]() 的平分线,利用等角的余角相等结合对顶角相等即可证得结论;
的平分线,利用等角的余角相等结合对顶角相等即可证得结论;
(2)利用正切函数求得AB=20,设![]() 的半径为R,在
的半径为R,在![]() 中,利用切线长定理求得AD=8,AO=16-R,根据勾股定理求得R的值,在
中,利用切线长定理求得AD=8,AO=16-R,根据勾股定理求得R的值,在![]() 中,求得
中,求得![]() ,利用正弦函数
,利用正弦函数![]() 即可求解.
即可求解.
(1)如图,连接![]() ,
,
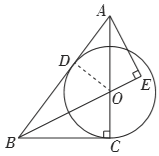
∵![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴BC是![]() 的切线,
的切线,
又![]() ,
,
∴![]() 为
为![]() 的平分线,
的平分线,
∴![]() ,
,
∵![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,![]() ,
,
∴AC=16,
∵![]() ,即
,即![]() ,
,
∴AB=20,
由(1)得,BD、BC都是![]() 切线,
切线,
∴BD=BC=12,
∴AD=AB-BD=20-12=8,
设![]() 的半径为R,
的半径为R,
在![]() 中,OD=R,AO=16-R,AD=8,
中,OD=R,AO=16-R,AD=8,
∵![]() ,即
,即![]() ,
,
∴R=6,
在![]() 中,BC=12,OC=6,
中,BC=12,OC=6,
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.

【题目】某社区为了加强社区居民对防护新型冠状病毒知识的了解,通过微信宣传防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据:
甲小区:85 80 95 100 90 95 85 65 75 85
90 90 70 90 100 80 80 90 95 75
乙小区:80 60 80 95 65 100 90 85 85 80
95 75 80 90 70 80 95 75 100 90
整理数据
成绩x(分) | 60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 |
甲小区 | 2 | 5 | a | b |
乙小区 | 3 | 7 | 5 | 5 |
分析数据
统计量 | 平均数 | 中位数 | 众数 |
甲小区 | 85.75 | 87.5 | c |
乙小区 | 83.5 | d | 80 |
应用数据
(1)填空:a= ,b= ,c= ,d= ;
(2)根据以上数据, (填“甲”或“乙”)小区对新型冠状病毒肺炎防护知识掌握得更好,理由是 (一条即可).
(3)若甲小区共有800人参加答卷,请估计甲小区成绩高于