题目内容
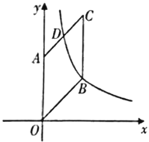
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 的直角顶点
的直角顶点![]() ,斜边
,斜边![]() 在
在![]() 轴上,且点
轴上,且点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上的一个动点,抛物线
边上的一个动点,抛物线![]() 过
过![]() ,
,![]() ,
,![]() 三点.
三点.
(1)当![]() 时,
时,
①求抛物线的解析式;
②平行于对称轴的直线![]() 与
与![]() 轴,
轴,![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,
,![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的值.
的值.
(2)以![]() 为等腰三角形顶角顶点,
为等腰三角形顶角顶点,![]() 为腰构造等腰
为腰构造等腰![]() ,且
,且![]() 点落在
点落在![]() 轴上.若在
轴上.若在![]() 轴上满足条件的
轴上满足条件的![]() 点有且只有一个时,请直接写出点
点有且只有一个时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)①![]() ;②
;②![]() 的值为
的值为![]() 或0;(2)
或0;(2)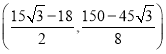 或
或![]() .
.
【解析】
(1)①先由A、C的坐标求出点D的坐标,由勾股定理求出AC,通过三角函数可求出DE,即可得到E点坐标,然后将D、E代入![]() 即可;②分
即可;②分![]() 和
和![]() 两种情况讨论,根据三角函数求解;
两种情况讨论,根据三角函数求解;
(2)分两种情况:①EG⊥AB,②以E为圆心DE为半径作圆,交AB延长线于M,过E作EH⊥AB于H, D、E、M三点共线时.
(1)①∵点![]() ,点
,点![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,
∴点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即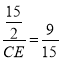 ,
,
∴![]() ,
,
∴![]() 的坐标为
的坐标为![]() ,即
,即![]() ,
,
把![]() 和D
和D![]() 代入
代入![]() ,
,
得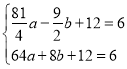 ,
,
解得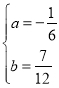 ,
,
∴抛物线的解析式为![]() .
.
②当![]() 时,可得
时,可得![]() ,
,
解得![]() ,
,
∴![]() ;
;
当![]() 时,可得
时,可得![]() ,
,
解得![]() ,
,
∴![]() .
.
综上所述,![]() 的值为
的值为![]() 或0.
或0.
(2)若在![]() 轴上满足条件的
轴上满足条件的![]() 点有且只有一个,则有两种情况,
点有且只有一个,则有两种情况,
第一种情况,EG⊥AB,如图,
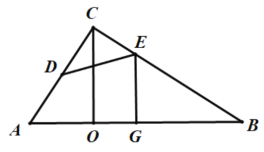
∠A+∠B=90°,∠B+∠BCO=90°,∠B+∠BEG=90°,
∴∠A=∠BCO=∠BEG,
∴△AOC∽△COB,△AOC∽△COB,
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在直角三角形CDE中,![]() ,
,
∴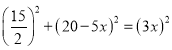 ,
,
解得![]() 或
或![]() (舍),
(舍),
![]() ,
,
由![]() ,
,![]() 得
得![]() ,
,![]() ,
,
∴![]() ,
,
∴E点坐标为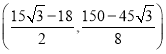 ,
,
第二种情况如图,以E为圆心DE为半径作圆,交AB延长线于M,过E作EH⊥AB于H, D、E、M三点共线时,
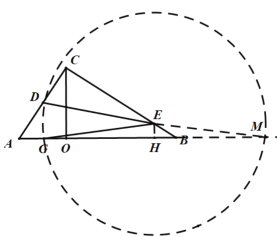
则E为DM的中点,
由D![]() 可知E的纵坐标为3,即EH=3,
可知E的纵坐标为3,即EH=3,
由题可知△EHB∽△COB,
∴![]() 即
即![]() ,
,
∴HB=4,OH=OB-HB=16-4=12,
∴E点坐标为![]() ,
,
∴答案为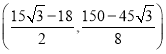 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案