Question

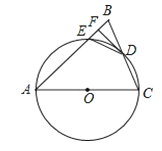
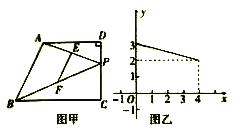
【题目】如图甲，在四边形ABCD中，AD//BC，∠C=90°动点P从点C出发沿线段CD向点D运动.到达点D即停止，若E、F分别是AP、BP的中点，设CP=x,△PEF的面积为y，且y与x之间的函数关系的图象如图乙所示，则线段AB长为（ ）

A.2B.2C.2D.2

Answer 1

【答案】C

【解析】

根据三角形中位线定理，得到S△PEF=S△ABP，由图像可以看出当x为最大值CD=4时，S△PEF=2，可求出AD=4，当x为0时，S△PEF=3，可求出BC=6；过点A作AG⊥BC于点G，根据勾股定理即可得解.

解：∵E、F分别为AP、BP的中点，

∴EF∥AB，EF=AB，

∴S△PEF=S△ABP，

根据图像可以看出x的最大值为4，

∴CD=4，

∵当P在D点时，△PEF的面积为2，

∴S△ABP=2×4=8，即S△ABD=8，

∴AD===4，

当点P在C点时，S△PEF=3，

∴S△ABP=3×4=12，即S△ABC=12，

∴BC===6，

过点A作AG⊥BC于点G，

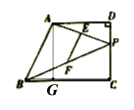
∴∠AGC=90°，

∵AD∥BC，

∴∠ADC+∠BCD=180°，

∵∠BCD=90°，

∴∠ADC=180°-90°=90°，

∴四边形AGCD是矩形，

∴CG=AD=4，AG=CD=4，

∴BG=BC-CG=6-4=2，

∴AB==2.

故选C.