Question

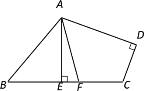
【题目】如图1，在△OAB中，∠OAB=90°，∠AOB=30°，OB=8．以OB为边，在△OAB

外作等边△OBC，D是OB的中点，连接AD并延长交OC于E．

（1）求证：四边形ABCE是平行四边形；

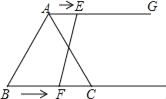
（2）如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长．

Answer 1

【答案】（1）见解析；（2）OG=1.

【解析】

（1）首先根据直角三角形中斜边上的中线等于斜边的一半可得DO=DA，再根据等边对等角可得∠DAO=∠DOA=30°，进而算出∠AEO=60°，再证明BC∥AE，CO∥AB，进而证出四边形ABCE是平行四边形．

（2）设OG=x，由折叠可得：AG=GC=8-x，再利用三角函数可计算出AO，再利用勾股定理计算出OG的长即可．

解：（1）证明：在Rt△OAB中，D为OB的中点，∴DO="DA" ．

∴∠DAO=∠DOA ="30°," ∠EOA="90°" ．∴∠AEO ="60°" ．

又∵△OBC为等边三角形，∴∠BCO=∠AEO =60°．∴BC∥AE．

∵∠BAO=∠COA =90°，∴OC∥AB．

∴四边形ABCE是平行四边形．

（2）设OG=x，由折叠可知：AG=GC=8－x．

在Rt△ABO中，∵∠OAB =90°，∠AOB =30°，OB=8，∴OA=OB·cos30°=8×=．

在Rt△OAG中，OG2+OA2=AG2，即，解得，．

∴OG=1．