题目内容
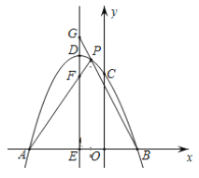
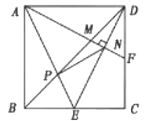
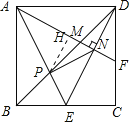
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上的一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则下列结论中:
①![]() ;②
;②![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④
;④![]() 正确的是()
正确的是()
A. ①②③B. ①②④C. ①③④D. ②③④
【答案】A
【解析】
利用正方形的性质,得出∠DAN=∠EDC,CD=AD,∠C=∠ADF即可判定△ADF≌△DCE(ASA),再证明△ABM∽△FDM,即可解答①;根据题意可知:AF=DE=AE=![]() ,再根据三角函数即可得出③;作PH⊥AN于H.利用平行线的性质求出AH=
,再根据三角函数即可得出③;作PH⊥AN于H.利用平行线的性质求出AH=![]() ,即可解答②;利用相似三角形的判定定理,即可解答④
,即可解答②;利用相似三角形的判定定理,即可解答④
解:∵正方形ABCD的边长为2,点E是BC的中点,
∴AB=BC=CD=AD=2,∠ABC=∠C=∠ADF=90°,CE=BE=1,
∵AF⊥DE,
∴∠DAF+∠ADN=∠ADN+∠CDE=90°,
∴∠DAN=∠EDC,
在△ADF与△DCE中,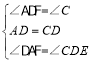 ,
,
∴△ADF≌△DCE(ASA),
∴DF=CE=1,
∵AB∥DF,
∴△ABM∽△FDM,
∴![]() ,
,
∴S△ABM=4S△FDM;故①正确;
根据题意可知:AF=DE=AE=![]() ,
,
∵![]() ×AD×DF=
×AD×DF=![]() ×AF×DN,
×AF×DN,
∴DN=![]() ,
,
∴EN=![]() ,AN=
,AN=![]() ,
,
∴tan∠EAF=![]() ,故③正确,
,故③正确,
作PH⊥AN于H.
∵BE∥AD,
∴![]() ,
,
∴PA=![]() ,
,
∵PH∥EN,
∴![]() ,
,
∴AH=![]() ,
,
∴PH=![]()
∴PN=![]() ,故②正确,
,故②正确,
∵PN≠DN,
∴∠DPN≠∠PDE,
∴△PMN与△DPE不相似,故④错误.
故选:A.

练习册系列答案
相关题目