题目内容
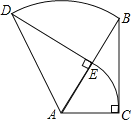
【题目】如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，AC＝2，将Rt△ABC绕点A逆时针旋转60°得到△ADE，则BC边扫过图形的面积为_____．
【答案】2π
【解析】
根据BC边扫过图形的面积是：S扇形DAB+S△ABC-S△ADE-S扇形ACE，分别求得：扇形BAD的面积、S△ABC以及扇形CAE的面积，即可求解．
∵∠C＝90°，∠BAC＝60°，AC＝2，
∴AB＝4，
扇形BAD的面积是：
＝
，
在直角△ABC中，BC＝ABsin60°＝4×
＝2
，AC＝2，
∴S△ABC＝S△ADE＝
ACBC＝×2×2＝2．
扇形CAE的面积是：
＝
，
则阴影部分的面积是：S扇形DAB+S△ABC﹣S△ADE﹣S扇形ACE
＝﹣
＝2π．
故答案为：2π．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某文具店购进一批纪念册，每本进价为20元，在销售过程中发现该纪念册每周的销售量y（本）与每本纪念册的售价x（元）之间具有某种函数关系，其对应规律如下表所示
售价x（元/本） | … | 22 | 23 | 24 | 25 | 26 | 27 | … |
销售量y（件） | … | 36 | 34 | 32 | 30 | 28 | 26 | … |
（1）请直接写出y与x的函数关系式： ．
（2）设该文店每周销售这种纪念册所获得的利润为W元，写出W与x之间的函数关系式，并求出该纪念册的销售单价定为多少元时，才能使文具店销售该纪念册每周所获利润最大？最大利润是多少？
