Question

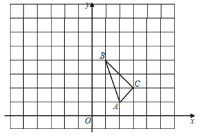
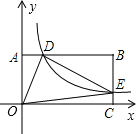
【题目】如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数y＝（x＞0）的图象与AB相交于点D．与BC相交于点E，且BD＝3，AD＝6，△ODE的面积为15，若动点P在x轴上，则PD+PE的最小值是_____．

Answer 1

【答案】．

【解析】

根据所给的三角形面积等于长方形面积减去三个直角三角形的面积，求得B和E的坐标，然后E点关于x的对称得E′，则E′（9，﹣4），连接DE′，交x轴于P，此时，PD+PE＝PD+PE′＝DE′最小，利用勾股定理即可求得E点关于x的对称得E′，则E′（9，﹣4），连接DE′，交x轴于P，此时，PD+PE＝PD+PE′＝DE′最小．

解：∵四边形OCBA是矩形，

∴AB＝OC，OA＝BC，

∵BD＝3，AD＝6，

∴AB＝9，

设B点的坐标为（9，b），

∴D（6，b），

∵D、E在反比例函数的图象上，

∴6b＝k，

∴E（9，b），

∵S△ODE＝S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE＝9b﹣k﹣k﹣3（b﹣b）＝15，

∴9b﹣6b﹣b＝15，

解得：b＝6，

∴D（6，6），E（9，4），

作E点关于x的对称得E′，则E′（9，﹣4），连接DE′，交x轴于P，此时，PD+PE＝PD+PE′＝DE′最小，

∵AB＝9，BE′＝6+4＝10，

∴DE′＝＝，

故答案为．