Question

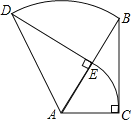
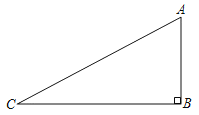
【题目】如图，在Rt△ABC中，∠ABC＝90°，AB＝2，BC＝4，点P在边BC上，联结AP，将△ABP绕着点A旋转，使得点P与边AC的中点M重合，点B的对应点是点B′，则BB′的长等于_____．

Answer 1

【答案】．

【解析】

如图，延长AB'交BC于E，过点B'作B'D⊥AB于点D，由勾股定理可求AC的长，由旋转的性质可求AP＝AM＝，∠PAB＝∠CAE，AB＝AB'＝2，通过证明△ABP∽△CBA，可得∠PAB＝∠C，可得CE＝AE，由勾股定理可求CE，BE的长，由相似三角形的性质可求B'D，BD的长，即可求解．

解：如图，延长AB'交BC于E，过点B'作B'D⊥AB于点D，

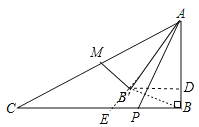
∵∠ABC＝90°，AB＝2，BC＝4，

∴AC＝2，

∵点M是AC中点，

∴AM＝，

∵将△ABP绕着点A旋转，使得点P与边AC的中点M重合，

∴AP＝AM＝，∠PAB＝∠CAE，AB＝AB'＝2，

∵AP2＝AB2+PB2，

∴PB＝1，

∵，且∠ABP＝∠ABC＝90°，

∴△ABP∽△CBA，

∴∠PAB＝∠C，

∴∠C＝∠CAE，

∴CE＝AE，

∵AE2＝AB2+BE2，

∴CE2＝4+（4﹣CE）2，

∴CE＝AE＝，

∴BE＝，

∵B'D∥BC，

∴△AB'D∽△AEB，

∴,

∴，

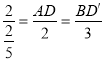∴AD＝，B'D＝，

∴BD＝，

∴BB'＝＝，

故答案为：．