题目内容
【题目】定义:在平面直角坐标系中,某个函数图象上任意两点的坐标分别为(x1,y1),(x2,y2),且x1≤x2,d=|y1-y2|.将这个函数图象在直线y=y1下方部分沿直线y=y1翻折,并将其向上平移d个单位,将这部分图象与原函数图象剩余部分的图象组成的新图象记为G,图象G对应的函数叫做这个函数的伴随函数.例如:点A(1,0)、B(2,1)在一次函数y=x-1的图象上,则它的伴随函数为![]() .
.
(1)点A、B在直线y=-2x上,点A在第二象限,点B在x轴上.当d=2时,求函数y=-2x的伴随函数所对应的函数表达式.
(2)二次函数y=x2-2x-3的图象交x轴负半轴交于点A,点B在抛物线上,设点B的横坐标为m.
①当d=0时,求该抛物线的伴随函数的图象G与直线y=4在第一象限的交点坐标;
②若直线y=2与该抛物线的伴随函数的图象G有四个交点,直接写出m的取值范围.
(3)抛物线y=x2-2nx+n2-n-1与y轴交于点A,点B在点A的左侧抛物线上,且d=1,当该抛物线的伴随函数的图象G上的点到x轴距离的最小值为1时,直接写出n的值.
【答案】(1)![]() ;(2)①图象G与直线y=4在第一象限的交点坐标为
;(2)①图象G与直线y=4在第一象限的交点坐标为![]() 或(1,4);②
或(1,4);②![]() 或
或![]() ;(3)n的值为-1或2.
;(3)n的值为-1或2.
【解析】
(1)点B在x轴上,故点B(0,0),d=2,则点A的纵坐标为2,求出点A的坐标,进而求解;
(2)①d=0,则m2﹣2m﹣3=0,则m=﹣1或m=3,故B(3,0),即可求解;②d=|m2﹣2m﹣3|<2,即可求解;
(3)①当点A在y轴下方时,翻折前的函数与x轴有交点,故图象G上的点到x轴距离的最小值为0,不合题意;②当点A在y轴上方时,图象G的最低点为点A,即n2﹣n﹣1=1,即可求解.
解:(1)∵点B在x轴上,
故点B(0,0),
∵d=2,则点A的纵坐标为2,
故2=-2x,
解得:x=-1,
故A(-1,2),
设翻折后的函数表达式为:y=2x+b,
将点A的坐标代入上式得:2=-2+b,
解得:b=4,
故翻折部分平移后函数的表达式为:y=2x+4+d=2x+6,
故伴随函数的表达式为:![]() ;
;
(2)y=x2-2x-3,令y=0,则x=-1或3,
故点A的坐标为:(-1,0),
设:B(m,m2-2m-3),
①d=0,则m2-2m-3=0,
∴m=-1或m=3,
∴B(3,0),
∴伴随函数为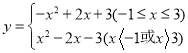 ;
;
当x<-1或x>3,y=4=x2-2x-3,
解得:![]() (舍去负值);
(舍去负值);
当-1≤x≤3时,y=4=-x2+2x+3,
解得:x=1;
∴图象G与直线y=4在第一象限的交点坐标为:![]() 或(1,4);
或(1,4);
②d=|m2-2m-3|<2,
∴-2<m2-2m-3<2,
∴![]() 或
或![]() ;
;
(3)y=x2-2nx+n2-n-1,
令x=0,则y=n2-n-1,
故点A(0,n2-n-1);
①当点A在y轴下方时,
翻折前的函数与x轴有交点,
故图象G上的点到x轴距离的最小值为0,不合题意;
②当点A在y轴上方时,
图象G的最低点为点A,即n2-n-1=1,
解得:n=-1或2,
故n的值为-1或2.

【题目】为了了解某校七年级学生每周上网的时间,甲、乙两名学生进行了抽样调查.甲同学调查了七年级电脑爱好者中40名学生每周上网的时间;乙同学从全校800名七年级学生中随机抽取了40名学生,调查了每周上网的时间.甲、乙同学各自整理的样本数据如表:
上网时间t(小时/周) | 甲学生抽样人数(人) | 乙学生抽样人数(人) |
0≤t<1.5 | 6 | 22 |
1.5≤t<2.5 | 10 | 10 |
2.5≤t<3.5 | 16 | 6 |
t≥3.5 | 8 | 2 |
(1)你认为哪名学生抽取的样本不合理,请说明理由.
(2)请你根据抽取样本合理的学生的数据,将调查结果绘制成合适的统计图(绘制一种即可).
(3)专家建议每周上网2.5小时以上(含2.5小时)的学生应适当减少上网的时间,估计该校全体七年级学生中应适当减少上网的时间的人数.