题目内容
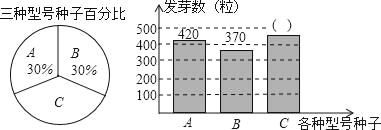
【题目】松山区种子培育基地用A,B,C三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图:
(1)求C型号种子的发芽数;
(2)通过计算说明,应选哪种型号的种子进行推广?
(3)如果将所有已发芽的种子放在一起,从中随机取出一粒,求取到C型号发芽种子的概率.
【答案】(1)480粒;(2)应选A型号的种子进行推广,理由见解析;(3)![]()
【解析】试题分析:(1)先求出C型号种子占的百分比,再求出C型号种子的数目,利用其发芽率为80%,即可求出其发芽的数目;
(2)分别计算三种种子的发芽率,选发芽率高的种子进行推广;
(3)求出在已发芽的种子中有A型号、B型号、C型号的数目,进而即可求出从中随机取出一粒,取到C型号发芽种子的概率.
试题解析:
(1)读图可知:C型号种子占1﹣30%﹣30%=40%,即1500×40%=600粒;
因为其发芽率为80%,故其发芽数是600×80%=480粒.
(2)A型号种子数为1500×30%=450,发芽率为: ![]() ×100%≈93%;
×100%≈93%;
B型号种子数为1500×30%=450,发芽率为: ![]() ×100%≈82%;
×100%≈82%;
C型号种子的发芽率为80%,
所以应选A型号的种子进行推广.
(3)在已发芽的种子中;有A型号的420粒,B型号的370粒,C型号的480粒;
故从中随机取出一粒,求取到C型号发芽种子的概率为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知点A,B在数轴上分别表示m,n,其中m<n.
(1)填写下表;
m | 3 | ﹣6 | ﹣5 |
n | 5 | 4 | ﹣4 |
A,B两点的距离 |
|
|
|
(2)若A,B两点的距离为d,则d与m,n的数量关系为 ;
(3)若S=|x﹣3|+|x﹣4|+|x﹣5|+…+|x﹣2018|,求S的最小值,并写出当S取最小值时x的取值范围.