题目内容
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.在Rt△ABC中,∠ACB=90°,AC=6,BC=8.点D是BC边上一点,连接AD,若△ABD是准互余三角形,则BD的长为_____.
【答案】5或![]()
【解析】
分两种情况画图说明,①根据△ABD是准互余三角形,可以证明AD是∠BAC的平分线,根据勾股定理即可求出BD的长;②可以根据△ABD是准互余三角形,证明△CAD∽△CBA,对应边成比例即可求出CD的长,进而求出BD的长.
解:∵∠ACB=90°,AC=6,BC=8,
∴AB=![]() =10.
=10.
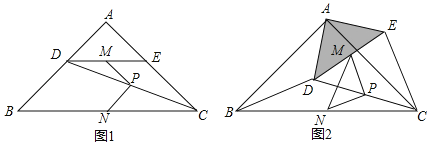
①如图1,
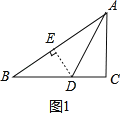
∵△ABD是准互余三角形,
∴∠B+2∠BAD=90°,
∵∠ACB=90°,
∴∠B+∠BAC=90°,
∴∠BAC=2∠BAD,
∴AD是∠BAC的平分线,
作DE⊥AB于点E,
则DC=DE,AE=AC=6,
设DC=DE=x,则BD=8﹣x,
BE=AB﹣AE=4,
在Rt△BDE中,根据勾股定理,得
BD2=DE2+BE2,
(8﹣x)2=x2+42,
解得x=3,
∴BD=BC﹣CD=8﹣3=5;
②如图2,
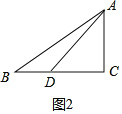
∵△ABD是准互余三角形,
∴2∠B+∠BAD=90°,
∵∠ACB=90°,
∴∠B+∠BAD+∠DAC=90°,
∴∠DAC=∠B,
∵∠C=∠C,
∴△CAD∽△CBA,
∴![]() ,
,
∴CD=![]() ,
,
∴BD=BC﹣CD=8﹣![]() =
=![]() .
.
综上所述:BD的长为5或![]() .
.
故答案为:5或![]() .
.

练习册系列答案
相关题目