题目内容
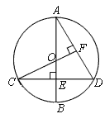
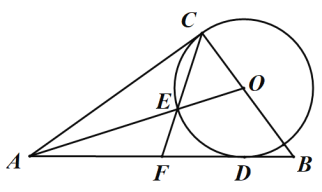
【题目】（1）如图，已知线段
和点O，利用直尺和圆规作
，使点O是的内心（不写作法，保留作图痕迹）；
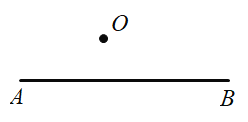
（2）在所画的中，若
，则的内切圆半径是______．
【答案】（1）作法：如图所示，见解析；（2）2．
【解析】
（1）内心是角平分线的交点，根据AO和BO分别是∠CAB和∠CBA的平分线，作图即可；
（2）连接OC，设内切圆的半径为r，利用三角形的面积公式，即可求出答案．
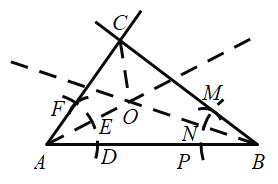
解：（1）作法：如图所示：
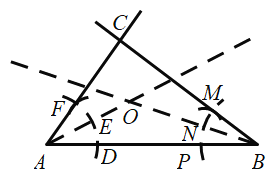
①作射线
、
；
②以点A为圆心，任意长为半径画弧分别交线段
，射线于点D，E；
③以点E为圆心，
长为半径画弧，交上一步所画的弧于点F，同理作出点M；
④作射线
，
相交于点C，
即所求．
（2）如图，连接OC，
∵
，
由勾股定理，得：
，
∴
；
∵
，
∴
，
∴
，
∴
，
∴的内切圆半径是2；
故答案为：2；
练习册系列答案
相关题目
