题目内容
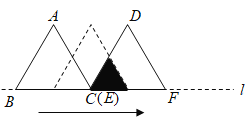
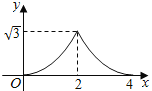
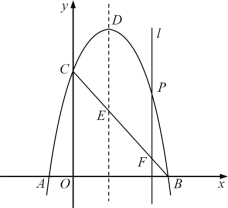
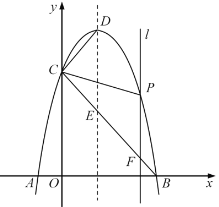
【题目】如图,二次函数y=ax2+bx+4的图象与x轴交于点A(-1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E.垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.
(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;
(2)在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;
(3)连接CP,CD,在移动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与![]() DCE相似,如果存在,求出点P的坐标,如果不存在,请说明理由.
DCE相似,如果存在,求出点P的坐标,如果不存在,请说明理由.
【答案】(1)y=-x2+3x+4,y=-x+4;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)运用待定系数法,利用A,B两点的坐标构建二元一次方程组求解二次函数的表达式,利用B,C两点的坐标确定直线BC的表达式;
(2)先求得DE的长,根据平行四边形的性质得到PF=DE,点P与点F的横坐标相同,故利用抛物线与直线的解析式表示它们的纵坐标,根据其差等于DE长构建一元二次方程求解;
(3)结合图形与已知条件,易于发现若两三角形相似,只可能存在△PCF∽△CDE一种情况.△CDE的三边均可求,(2)中已表示PF的长,再构建直角三角形或借助两点间距离公式,利用勾股定理表示出CF的长,这样根据比例式列方程求解,从而可判断点P是否存在,以及求解点P的值.
(1)由题意,将A(-1.0),B(4.0)代入![]() ,得
,得
![]() ,解得
,解得![]() ,
,
∴二次函数的表达式为![]() ,
,
当![]() 时,y=4,
时,y=4,
∴点C的坐标为(0,4),又点B的坐标为(4,0),
设线段BC所在直线的表达式为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴BC所在直线的表达式为![]() ;
;
(2)∵DE⊥x轴,PF⊥x轴,
∴DE∥PF,
只要DE=PF,此时四边形DEFP即为平行四边形.
由二次函数y=-![]() +3
+3![]() +4=(
+4=(![]() -
-![]() ) 2+
) 2+![]() ,得D的坐标为(
,得D的坐标为(![]() ,
,![]() ),
),
将![]() 代入
代入![]() ,即y=-
,即y=-![]() +4=
+4=![]() ,得点E的坐标为(
,得点E的坐标为(![]() ,
,![]() ),
),
∴DE=![]() -
-![]() =
=![]() ,
,
设点P的横坐标为t,则P(t,-t2+3t+4),F(t,-t+4),
PF=-t2+3t+4-(-t+4)=-t2+4t,
由DE=PF,得-t2+4t=![]() ,
,
解之,得t1=![]() (不合题意,舍去),t2=
(不合题意,舍去),t2=![]() ,
,
当t=![]() 时,-t2+3t+4=-(
时,-t2+3t+4=-(![]() )2+3×
)2+3×![]() +4=
+4=![]() ,
,
∴P的坐标为(![]() ,
,![]() );
);
(3)由(2)知,PF∥DE,
∴∠CED=∠CFP,
又∠PCF与∠DCE有共同的顶点C,且∠PCF在∠DCE的内部,
∴∠PCF≠∠DCE,
∴只有当∠PCF=∠CDE时,△PCF∽△CDE,
由D (![]() ,
,![]() ),C(0,4),E(
),C(0,4),E(![]() ,
,![]() ),利用勾股定理,可得
),利用勾股定理,可得
CE=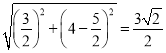 ,DE=
,DE=![]() ,
,
由(2)以及勾股定理知,PF=-t2+4t,F(t,-t+4),
CF=![]() ,
,
∵△PCF∽△CDE,
∴![]() ,即
,即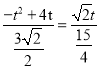 ,
,
∵t≠0,
∴![]() (
(![]() )=3,
)=3,
∴t=![]() ,
,
当t=![]() 时,-t2+3t+4=-(
时,-t2+3t+4=-(![]() )2+3×
)2+3×![]() +4=
+4=![]() .
.
∴点P的坐标是(![]() ,
,![]() ).
).

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案