题目内容
【题目】如图，已知∠MON＝30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1B2，△A2B2B3，△A3B3B4，…均为等边三角形．若OB1＝1，则△A8B8B9的边长为（ ）
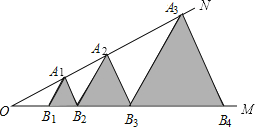
A.64B.128C.132D.256
【答案】B
【解析】
根据等腰三角形的性质以及平行线的性质得出
，以及
，得出
，
，
进而得出答案．
解：∵△A1B1B2是等边三角形，
∴∠A1B1B2＝∠A1B2O＝60°，A1B1＝A1B2，
∵∠O＝30°，
∴∠A2A1B2＝∠O+∠A1B2O＝90°，
∵∠A1B1B2＝∠O+∠OA1B1，
∴∠O＝∠OA1B1＝30°，
∴OB1＝A1B1＝A1B2＝1，
在Rt△A2A1B2中，∵∠A1A2B2＝30°
∴A2B2＝2A1B2＝2，
同法可得A3B3＝22，A4B4＝23，…，AnBn＝2n﹣1，
∴△A8B8B9的边长＝27＝128，
故选：B．
练习册系列答案
相关题目
【题目】九年级（1）班全班50名同学组成五个不同的兴趣爱好小组，每人都参加且只能参加一个小组，统计（不完全）人数如下表：
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是
．
解答下列问题：
（1）
．
（2）补全条形统计图：
（3）若从第一组和第五组中任选两名同学，求这两名同学是同一组的概率．（用树状图或列表把所有可能都列出来）
