��Ŀ����
����Ŀ����ͼ��1������A��B��C���ֲ�ͬ�ͺŵĿ�Ƭ�����ţ�����A���DZ߳�Ϊa��a��b���������Σ�B���dz�Ϊa����Ϊb�ij����Σ�C���DZ߳�Ϊb�������Σ�

��1������A�Ϳ�Ƭ1�ţ�B�Ϳ�Ƭ2�ţ�C�Ϳ�Ƭ1��ƴ����һ�������Σ���ͼ��2�������������εı߳�Ϊ�� �������ݸ�ͼ����д��һ��������ʽ�ֽ�ĵ�ʽ���� ����
��2����Ҫƴһ����Ϊ2a+b����Ϊa+2b�ij����Σ�����ҪA�Ƭx�ţ�B�Ƭy�ţ�C�Ƭz�ţ���x+y+z���� ����
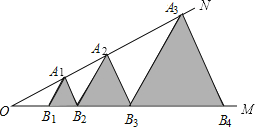
��3������A�Ϳ�Ƭ1�ţ�B�Ϳ�Ƭ6�ţ�C�Ϳ�Ƭ11�ţ�����18�ſ�Ƭ���õ����ſ�Ƭ�����µĿ�Ƭȫ���ϣ�����ƴ��һ�������λ����������м���ƴ��������ͨ������˵�����ɣ�
���𰸡���1��a+b��a2+2ab+b2����a+b��2����2��9����3������ƴ������һ�֣�A�Ϳ�Ƭ�õ�1�ţ�B�Ϳ�Ƭ�õ�1�ţ���ƴ��һ�������Σ��ڶ��֣�A�Ϳ�Ƭ�õ�1�ţ�C�Ϳ�Ƭ�õ�1�ţ���ƴ��һ�������Σ����������2��ƴ���������֣�C�Ϳ�Ƭ�õ�2�ţ�����ƴ��һ�������η��Σ�
��������
��1����ͼ�ɵÿɵ������εı߳�Ϊ![]() ����ͼ��2���ɵ���ʽ�ֽ�ĵ�ʽ
����ͼ��2���ɵ���ʽ�ֽ�ĵ�ʽ![]() ��
��
��2����Ϊ![]() ��������Ҫ��
��������Ҫ��![]() �Ƭ2�ţ�
�Ƭ2�ţ�![]() �Ƭ5�ţ�
�Ƭ5�ţ�![]() �Ƭ2�ţ�������
�Ƭ2�ţ�������![]() ��
��![]() ��
��![]() ��Ӧ��ֵ��
��Ӧ��ֵ��
��3����һ�֣�![]() �Ϳ�Ƭ�õ�1�ţ�
�Ϳ�Ƭ�õ�1�ţ�![]() �Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ
�Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ![]() ����Ϊ
����Ϊ![]() ��
��
�ڶ��֣�![]() �Ϳ�Ƭ�õ�1�ţ�
�Ϳ�Ƭ�õ�1�ţ�![]() �Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ
�Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ![]() ����Ϊ
����Ϊ![]() ��
��
�����֣�![]() �Ϳ�Ƭ�õ�2�ţ�����ƴ��һ�������η��Σ��������α߳�Ϊ
�Ϳ�Ƭ�õ�2�ţ�����ƴ��һ�������η��Σ��������α߳�Ϊ![]() ��
��
�⣺��1����ͼ��1����ͼ��2���ɵ������εı߳�Ϊ a+b��
��ͼ��2���ɵ���ʽ�ֽ�ĵ�ʽa2+2ab+b2����a+b��2��
�ʴ�Ϊa+b��a2+2ab+b2����a+b��2��
��2���ߣ�2a+b����a+2b����2a2+5ab+2b2��
����Ҫ��A�Ƭ2�ţ�B�Ƭ5�ţ�C�Ƭ2�ţ�
��x+y+z��2+5+2��9��
�ʴ�Ϊ9��
��3������ƴ����
��һ�֣�A�Ϳ�Ƭ�õ�1�ţ�B�Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ5A+11b����Ϊb��
��b��5a+11b����5ab+11b2��
�ڶ��֣�A�Ϳ�Ƭ�õ�1�ţ�C�Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ3A+5b����Ϊ2b��
��2b��3a+5b����6ab+10b2�����߳�Ϊ6A+10b����Ϊb���ࣨ6a+10b��b��6ab+10b2�����������2��ƴ����
�����֣�C�Ϳ�Ƭ�õ�2�ţ�����ƴ��һ�������η��Σ��������α߳�ΪA+3b��
�ࣨa+3b��2��a2+6ab+9b2��

 �����ҵ���������ϵ�д�
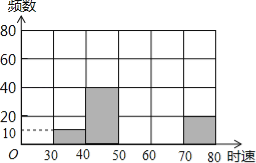
�����ҵ���������ϵ�д�����Ŀ����ij�״����������һ��������ʱ�������������õ���Ƶ���ֲ�����δ��ɣ���
���ݶ� | 30��40 | 40��50 | 50��60 | 60��70 | 70��80 | �ܼ� |
Ƶ �� | 10 | 40 | | | 20 | |
�ٷֱ� | 5% | | 40% | | 10% | |
ע��30��40Ϊʱ�ٴ��ڵ���30ǧ��С��40ǧ�ף�������ͬ��
��1������ѱ��е�������д������
��2����ȫƵ���ֲ�ֱ��ͼ��
��3�������·������ʱ�ٳ���60ǧ��ΪΥ�£���Υ�³������ж�������