题目内容
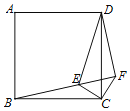
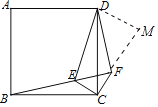
【题目】如图，在正方形ABCD内一点E连接BE、CE，过C作CF⊥CE与BE延长线交于点F，连接DF、DE．CE＝CF＝1，DE＝
，下列结论中：①△CBE≌△CDF；②BF⊥DF；③点D到CF的距离为2；④S四边形DECF＝
+1．其中正确结论的个数是（ ）
A.1B.2C.3D.4
【答案】B
【解析】
根据正方形的性质、全等三角形的判定和性质、勾股定理等知识逐项判断即可．
解：∵四边形ABCD是正方形，
∴BC＝CD，∠BCD＝90°，
∵CF⊥CE，
∴∠ECF＝∠BCD＝90°，
∴∠BCE＝∠DCF，
在△BCE与△DCF中，
，
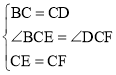∴△BCE≌△DCF（SAS），
故①正确；
∵△BCE≌△DCF，
∴∠CBE＝∠CDF，
∴∠DFB＝∠BCD＝90°，
∴BF⊥ED，
故②正确，
过点D作DM⊥CF，交CF的延长线于点M，
∵∠ECF＝90°，FC＝EC＝1，
∴∠CFE＝45°，
∵∠DFM+∠CFB＝90°，
∴∠DFM＝∠FDM＝45°，
∴FM＝DM，
∴由勾股定理可求得：EF＝
，
∵DE＝
，
∴由勾股定理可得：DF＝2，
∵EF2+BE2＝2BE2＝BF2，
∴DM＝FM＝，故③错误，
∵△BCE≌△DCF，
∴S△BCE＝S△DCF，
∴S四边形DECF＝S△DCF+S△DCE
＝S△ECF+S△DEF
＝S△AFP+S△PFB
＝
，故④错误，
故选：B．
练习册系列答案
相关题目
