题目内容
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
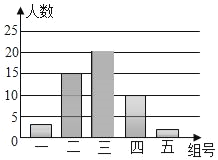
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)

【答案】(1)5;(2)补全条形统计图见解析;(3)这两名同学是同一组的概率为![]() .
.
【解析】
(1)用全班人数减去二、三、四组的人数即可得;
(2)根据第三组数据补全条形图即可;
(3)先求出a、b的值,然后画树状图得到所有等可能的情况数,找出符合条件的情况数,利用概率公式求解即可.
(1)由题意知![]() ,
,
故答案为:5;
(2)补全图形如下:
(3)∵a:15=1:5,
∴![]() ,
,
∴![]() =2,
=2,
即第一组有3名同学,第五组有2名同学,
设第一组3位同学分别为![]() ,设第五组2位同学分别为
,设第五组2位同学分别为![]() ,
,

由上图可知,一共有20种等可能的结果,其中两名同学是同一组的有8种,所求概率是:![]() .
.

【题目】高速公路某收费站出城方向有编号为![]() 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
收费出口编号 |
|
|
|
|
|
通过小客车数量(辆) | 260 | 330 | 300 | 360 | 240 |
在![]() 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
【题目】从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
用时的频数 用时 线路 |
|
|
| 合计 |
3路 | 260 | 167 | 23 | 450 |
121路 | 160 | 166 | 124 | 450 |
26路 | 50 | 122 | 278 | 450 |
早高峰期间,乘坐__________(“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.