题目内容
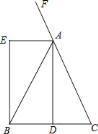
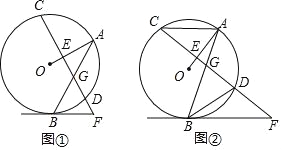
【题目】在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B作⊙O的切线BF交CD的延长线于点F.
(I)如图①,若∠F=50°,求∠BGF的大小;
(II)如图②,连接BD,AC,若∠F=36°,AC∥BF,求∠BDG的大小.
【答案】(I)65°;(II)72°
【解析】
(I)如图①,连接OB,先利用切线的性质得∠OBF=90°,而OA⊥CD,所以∠OED=90°,利用四边形内角和可计算出∠AOB=130°,然后根据等腰三角形性质和三角形内角和计算出∠1=∠A=25°,从而得到∠2=65°,最后利用三角形内角和定理计算∠BGF的度数;
(II)如图②,连接OB,BO的延长线交AC于H,利用切线的性质得OB⊥BF,再利用AC∥BF得到BH⊥AC,与(Ⅰ)方法可得到∠AOB=144°,从而得到∠OBA=∠OAB=18°,接着计算出∠OAH=54°,然后根据圆周角定理得到∠BDG的度数.
解:(I)如图①,连接OB,
∵BF为⊙O的切线,
∴OB⊥BF,
∴∠OBF=90°,
∵OA⊥CD,
∴∠OED=90°,
∴∠AOB=180°﹣∠F=180°﹣50°=130°,
∵OA=OB,
∴∠1=∠A=![]() (180°﹣130°)=25°,
(180°﹣130°)=25°,
∴∠2=90°﹣∠1=65°,
∴∠BGF=180°﹣∠2﹣∠F=180°﹣65°﹣50°=65°;
(II)如图②,连接OB,BO的延长线交AC于H,
∵BF为⊙O的切线,
∴OB⊥BF,
∵AC∥BF,
∴BH⊥AC,
与(Ⅰ)方法可得到∠AOB=180°﹣∠F=180°﹣36°=144°,
∵OA=OB,
∴∠OBA=∠OAB=![]() (180°﹣144°)=18°,
(180°﹣144°)=18°,
∵∠AOB=∠OHA+∠OAH,
∴∠OAH=144°﹣90°=54°,
∴∠BAC=∠OAH+∠OAB=54°+18°=72°,
∴∠BDG=∠BAC=72°.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
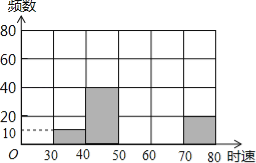
单元期中期末卷系列答案【题目】将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):
数据段 | 30~40 | 40~50 | 50~60 | 60~70 | 70~80 | 总计 |
频 数 | 10 | 40 | | | 20 | |
百分比 | 5% | | 40% | | 10% | |
注:30~40为时速大于等于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段汽车时速超过60千米即为违章,则违章车辆共有多少辆?