题目内容
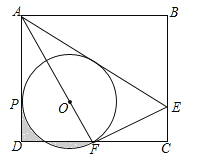
【题目】如图,已知⊙![]() 为正三角形
为正三角形![]() 的内切圆,
的内切圆,![]() 为切点,四边形
为切点,四边形![]() 是⊙
是⊙![]() 的内接正方形,
的内接正方形,![]() ,则正三角形
,则正三角形![]() 的边长为( )
的边长为( )

A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
如图,连接OD、OE、OC,已知四边形![]() 是⊙
是⊙![]() 的内接正方形,可得EF=ED=
的内接正方形,可得EF=ED=![]() ,∠EOD=90°,根据勾股定理可得OD=OE=1;再由⊙
,∠EOD=90°,根据勾股定理可得OD=OE=1;再由⊙![]() 为正三角形
为正三角形![]() 的内切圆,
的内切圆,![]() 为切点,可得∠ODC=90°,∠OCD=30°,即可得OC=2,CD=
为切点,可得∠ODC=90°,∠OCD=30°,即可得OC=2,CD=![]() ;
;![]() 为正三角形
为正三角形![]() 的内心,也为正三角形
的内心,也为正三角形![]() 的外心,由此即可求得AD=2CD=2
的外心,由此即可求得AD=2CD=2![]() .
.
如图,连接OD、OE、OC,

∵四边形![]() 是⊙
是⊙![]() 的内接正方形,
的内接正方形,
∴EF=ED=![]() ,∠EOD=90°,
,∠EOD=90°,
∴OD=OE=1;
∵⊙![]() 为正三角形
为正三角形![]() 的内切圆,
的内切圆,![]() 为切点,
为切点,
∴∠ODC=90°,∠OCD=30°,
∴OC=2,CD=![]() ;
;
∵![]() 为正三角形
为正三角形![]() 的内心,
的内心,
∴![]() 也为正三角形
也为正三角形![]() 的外心,
的外心,
∴AD=2CD=2![]() .
.
故选C.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目