题目内容
【题目】如图,![]() ,
,![]() 是
是![]() 内一点,
内一点,![]() .若
.若![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点,则
上的动点,则![]() 周长的最小值为_______.
周长的最小值为_______.

【答案】10
【解析】
作点P关于OB的对称点P′,点P关于OA的对称点P″,连接P′P″交OB于R,交OA于Q,连接PR、PQ,如图3,利用对称的性质得到△PQR周长=P′P″,根据两点之间线段最短可判断此时△PQR周长最小,最小值为P′P″的长,再证明△P′OP″为等边三角形得到P′P″=OP′=OP=10,从而得到△PQR周长的最小值
解:
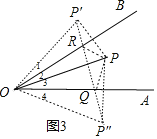
作点P关于OB的对称点P′,点P关于OA的对称点P″,连接P′P″交OB于R,交OA于Q,连接PR、PQ,如图3,
则OP=OP′,OP=OP″,RP=RP′,QP=QP″,
∴△PQR周长=PR+RQ+PQ=RP′+RQ+QP″=P′P″,
∴此时△PQR周长最小,最小值为P′P″的长,
∵由对称性可知OP=OP′,OP=OP″,PP′⊥OB,PP″⊥OA,
∴∠1=∠2,∠3=∠4,
∴∠P′OP″=∠1+∠2+∠3+∠4=2∠2+2∠3=2∠BOA=60°,
∴△P′OP″为等边三角形,
∴P′P″=OP′=OP=10,
故答案是:10.

练习册系列答案
相关题目
【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?