题目内容
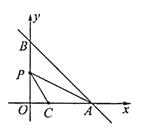
【题目】如图,在Rt△ABC中,∠C=30°,将△ABC绕点B旋转α(0<α<60°)到△A′BC′,边AC和边A′C′相交于点P,边AC和边BC′相交于Q.当△BPQ为等腰三角形时,则α=__________.

【答案】20°或40°
【解析】
过B作BD⊥AC于D,过B作BE⊥A'C'于E,根据旋转可得△ABC≌△A'BC',则BD=BE,进而得到BP平分∠A'PC,再根据∠C=∠C'=30°,∠BQC=∠PQC',可得∠CBQ=∠C'PQ=θ,即可得出∠BPQ=![]() (180°-∠C'PQ)=90°-
(180°-∠C'PQ)=90°-![]() θ,分三种情况讨论,利用三角形内角和等于180°,即可得到关于θ的方程,进而得到结果.
θ,分三种情况讨论,利用三角形内角和等于180°,即可得到关于θ的方程,进而得到结果.
如图,过B作BD⊥AC于D,过B作BE⊥A'C'于E,
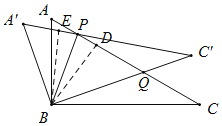
由旋转可得,△ABC≌△A'BC',则BD=BE,
∴BP平分∠A'PC,
又∵∠C=∠C'=30°,∠BQC=∠PQC',
∴∠CBQ=∠C'PQ=θ,
∴∠BPQ=![]() (180°-∠C'PQ)=90°-
(180°-∠C'PQ)=90°-![]() θ,
θ,
分三种情况:
①如图所示,当PB=PQ时,∠PBQ=∠PQB=∠C+∠QBC=30°+θ,
∵∠BPQ+∠PBQ+∠PQB=180°,
∴90°-![]() θ+2×(30°+θ)=180°,
θ+2×(30°+θ)=180°,
解得θ=20°;
②如图所示,当BP=BQ时,∠BPQ=∠BQP,
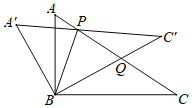
即90°-![]() θ=30°+θ,
θ=30°+θ,
解得θ=40°;
③当QP=QB时,∠QPB=∠QBP=90°-![]() θ,
θ,
又∵∠BQP=30°+θ,
∴∠BPQ+∠PBQ+∠BQP=2(90°-![]() θ)+30°+θ=210°>180°(不合题意),
θ)+30°+θ=210°>180°(不合题意),
故答案为:20°或40°.

练习册系列答案
相关题目