Question

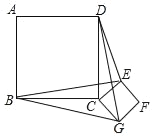
【题目】如图，AB为⊙O的直径，弦BC，DE相交于点F，且DE⊥AB于点G，过点C作⊙O的切线交DE的延长线于点H．

（1）求证：HC=HF；

（2）若⊙O的半径为5，点F是BC的中点，tan∠HCF=m，写出求线段BC长的思路．

Answer 1

【答案】（1）证明见解析；（2）求解思路见解析.

【解析】

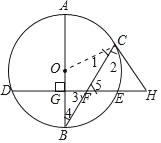
(1)连接OC，如图1，由切线的性质可得∠2+∠1=90°，由DE⊥AB，可得∠3+∠4=90°，继而结合OB=OC可得到∠2=∠5，由此即可证得结论；

（2）思路一：连接OF，如图2，由垂径定理可得BC=2CF，∠OFC=90°，由∠6与∠1互余，∠2与∠1互余可推导得出tan∠6=m，在Rt△OFC中，由tan∠6==m，可设OF=x，CF=mx，由勾股定理，可解得x的值，由BC=2CF=2mx，可求BC的长；

思路二：连接AC，如图3，由AB是⊙O的直径，可得出∠6与∠4互余，继而可得∠6=∠3，由∠6=∠3，∠3=∠2，从而可知tan∠6=m，③在Rt△ACB中，由tan∠6==m，，可设AC=x，BC=mx，由勾股定理，可解得x的值，由BC=mx，可求BC的长．

（1）连接OC，如图1，

∵CH是⊙O的切线，

∴∠2+∠1=90°，

∵DE⊥AB，

∴∠3+∠4=90°，

∵OB=OC，

∴∠1=∠4，

∴∠2=∠3，

又∵∠5=∠3，

∴∠2=∠5，

∴HC=HF；

（2）求解思路如下：

思路一：连接OF，如图2．

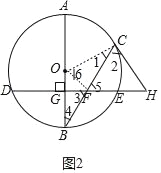
①OF过圆心且点F是BC的中点，由垂径定理可得BC=2CF，∠OFC=90°；

②由∠6与∠1互余，∠2与∠1互余可得∠6=∠2，从而可知tan∠6=m；

③在Rt△OFC中，由tan∠6==m，可设OF=x，CF=mx，由勾股定理，得x2+（mx）2=52，可解得x的值；

④由BC=2CF=2mx，可求BC的长．

思路二：连接AC，如图3．

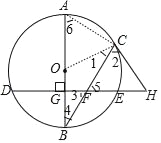
①由AB是⊙O的直径，可得△ACB是直角三角形，知∠6与∠4互余，

又DE⊥AB可知∠3与∠4互余，得∠6=∠3；

②由∠6=∠3，∠3=∠2，可得∠6=∠2，从而可知tan∠6=m；

③在Rt△ACB中，由tan∠6==m，，可设AC=x，BC=mx，

由勾股定理，得x2+（mx）2=102，可解得x的值；

④由BC=mx，可求BC的长．