题目内容
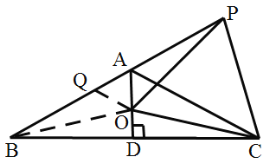
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 延长线上一点,点
延长线上一点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④
是等边三角形;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.1B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
①②连接OB,根据垂直平分线性质即可求得OB=OC=OP,即可解题;
③根据周角等于360°和三角形内角和为180°即可求得∠POC=2∠ABD=60°,即可解题;
④AB上找到Q点使得AQ=OA,易证△BQO≌△PAO,可得PA=BQ,即可解题.
连接![]() ,
,

∵![]() ,AD⊥BC,
,AD⊥BC,
∴![]() 是
是![]() 垂直平分线,
垂直平分线,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵AB=AC,∠BAC=120
∴![]()
∴![]() ,
,
∴![]() .
.
故①②正确;
∵![]() 中,
中,![]() ,
,
![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
故③正确;
在AB上找到Q点使得AQ=OA,
则![]() 为等边三角形,
为等边三角形,
则![]() ,
,
在![]() 和
和![]() 中,
中,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,故④正确.
,故④正确.
故选:D.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?