题目内容
【题目】(2017四川省达州市,第16题,3分)如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④
CE;④![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
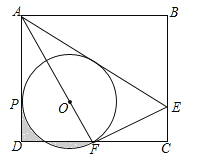
【答案】①②④.
【解析】解:①∵AF是AB翻折而来,∴AF=AB=6.∵AD=BC=![]() ,∴DF=
,∴DF=![]() =3,∴F是CD中点;∴①正确;
=3,∴F是CD中点;∴①正确;
②连接OP,∵⊙O与AD相切于点P,∴OP⊥AD.∵AD⊥DC,∴OP∥CD,∴ ![]() ,设OP=OF=x,则
,设OP=OF=x,则![]() ,解得:x=2,∴②正确;
,解得:x=2,∴②正确;
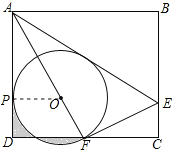
③∵Rt△ADF中,AF=6,DF=3,∴∠DAF=30°,∠AFD=60°,∴∠EAF=∠EAB=30°,∴AE=2EF.∵∠AFE=90°,∴∠EFC=90°﹣∠AFD=30°,∴EF=2EC,∴AE=4CE,∴③错误;
④连接OG,作OH⊥FG,∵∠AFD=60°,OF=OG,∴△OFG为等边△.同理△OPG为等边△,∴∠POG=∠FOG=60°,OH=![]() OG=
OG=![]() ,S扇形OPG=S扇形OGF,∴S阴影=(S矩形OPDH﹣S扇形OPG﹣S△OGH)+(S扇形OGF﹣S△OFG)=S矩形OPDH﹣
,S扇形OPG=S扇形OGF,∴S阴影=(S矩形OPDH﹣S扇形OPG﹣S△OGH)+(S扇形OGF﹣S△OFG)=S矩形OPDH﹣![]() S△OFG=
S△OFG=![]() =
=![]() ,∴④正确;
,∴④正确;
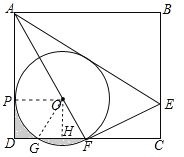
故答案为:①②④.

【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?