题目内容
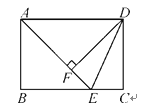
【题目】如图,已知:在平行四边形ABCD中,AB=2,AD=4,∠ABC=60°,E为AD上一点,连接CE,AF∥CE且交BC于点F.
(1)求证:四边形AECF为平行四边形.
(2)证明:△AFB≌△CE D.
(3)DE等于多少时,四边形AECF为菱形.
(4)DE等于多少时,四边形AECF为矩形.

【答案】(1)见解析;(2)见解析;(3)DE=2;(4)DE=1.
【解析】
(1)根据两组对边分别平行的四边形是平行四边形进行证明即可得;
(2)根据ABCD为平行四边形,可得AB=CD, AD=BC,再根据AECF为平行四边形,可得AF=CE,AE=FC,继而可得DE=BF,根据SSS即可证明△AFB≌△CED;
(3)当DE=2时,AECF为菱形,理由:由AB=DC=2,∠ABC=∠EDC=60°可得△EDC为等边三角形,继而可得到AE=EC,根据邻边相等的平行四边形是菱形即可得;
(4)当DE=1时,AECF为矩形,理由:若AECF为矩形则有∠DEC=90°,再根据DC=2,∠D=60°,则可得∠DCE=30°,继而可得DE=1.
(1)∵![]() 为平行四边形,∴
为平行四边形,∴![]() ,即
,即![]() ,
,
又∵![]() (已知),∴
(已知),∴![]() 为平行四边形;
为平行四边形;
(2)∵![]() 为平行四边形,∴
为平行四边形,∴![]() ,
, ![]() ,
,
∵![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
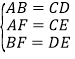 ,
,
∴![]() ;
;
(3)当![]() 时,
时,![]() 为菱形,理由如下:
为菱形,理由如下:
∵![]() ,
,
∴![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,即:
,即:![]() ,
,
∴平行四边形![]() 为菱形;
为菱形;
(4)当![]() 时,
时,![]() 为矩形,理由如下:
为矩形,理由如下:
若![]() 为矩形得:
为矩形得:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目