Question

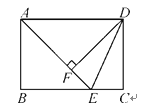
【题目】如图，在长方形ABCD中，点E是BC边上的点，AE＝BC，DF⊥AE，垂足为点F，连接DE.

(1)求证：AB＝DF；

(2)求证：DE平分∠AEC.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）由矩形的性质得出对边相等，对边平行，四个角为90°，然后由平行线的性质得出∠AEB=∠DAF，根据AAS可证得△ABE≌△DFA，根据全等三角形的对应边相等即可得出结论；

（2）利用HL证明Rt△DFE≌Rt△DCE即可得出结论．

（1）∵四边形ABCD是长方形，

∴AD＝BC，AD∥BC，∠B＝∠C＝90°，

∴∠AEB＝∠DAF.

又AE＝BC，

∴AE＝AD.

∵DF⊥AE，

∴∠DFA ＝90° ＝∠B，

在△ABE和△DFA中，

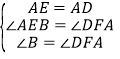
∴△ABE≌△DFA(AAS)，

∴AB＝DF；

（2）∵AB＝DF，AB＝DC，

∴DF＝DC.

又DE＝DE，

∴Rt△DFE≌Rt△DCE(HL)，

∴∠DEF＝∠DEC，

即DE平分∠AEC.