Question

【题目】如图，在△ABC中，AD平分∠BAC，且BD=CD，DE⊥AB于点E，DF⊥AC于点F．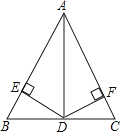

（1）求证：AB=AC；
（2）若AD=2 ，∠DAC=30°，求AC的长．

Answer 1

【答案】
（1）

证明：

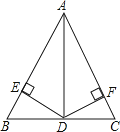
∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，

∴DE=DF，∠DEB=∠DFC=90°，

在RT△DEB和RT△DFC中，

，

∴△DEB≌△DFC，

∴∠B=∠C，

∴AB=AC

（2）

解：∵AB=AC，BD=DC，

∴AD⊥BC，

在RT△ADC中，∵∠ADC=90°，AD=2 ，∠DAC=30°，

∴AC=2CD，设CD=a，则AC=2a，

∵AC2=AD2+CD2，

∴4a2=a2+（2 ）2，

∵a＞0，

∴a=2，

∴AC=2a=4．

【解析】（1）先证明△DEB≌△DFC得∠B=∠C由此即可证明．（2）先证明AD⊥BC，再在RT△ADC中，利用30°角性质设CD=a，AC=2a，根据勾股定理列出方程即可解决问题．本题考查全等三角形的判定和性质、直角三角形30°性质、勾股定理等知识，解题的关键是正确寻找全等三角形，记住直角三角形30°角所对的直角边等于斜边的一半，属于中考常考题型．