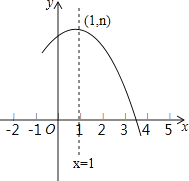��Ŀ����
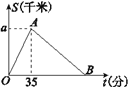
����Ŀ��2016��3��27������ˮ��������ɾ��������������У�ij�˶�Ա�������ع㳡���ų�����;���Ͻ���ţ��ر���·���ܻ��յ���ع㳡���ţ�����˶�Ա�뿪����·��S(ǧ��)���ܲ�ʱ��t(����)֮��ĺ�����ϵ��ͼ��ʾ�����д���㵽�Ͻ���ŵ�ƽ���ٶ���0.3ǧ��/�֣���ʱ35���ӣ�����ͼ���ṩ����Ϣ������������⣺
(1)��ͼ��a��ֵ��
(2)��ί���ھ������2.1ǧ�״�����һ�������C�����˶�Ա�ӵ�һ�ι�C�㵽�ڶ��ι�C�����õ�ʱ��Ϊ68���ӣ�
����AB����ֱ�ߵĺ�������ʽ��
�ڸ��˶�Ա����������ʱ���ٷ��ӣ�
���𰸡�(1) a��10.5ǧ��;(2)��S�䣽��0.21t��17.85;��85���ӣ�
��������������1������·��=�ٶȡ�ʱ�䣬���ɽ�����⣮
��2���������A��B�������꼴�ɽ�����⣮
����s=0����t��ֵ���ɽ��������
����������⣺��1��������㵽�Ͻ���ŵ�ƽ���ٶ���0.3ǧ��/�֣���ʱ35���ӣ���a=0.3��35=10.5ǧ�ף�
��2���١��߶�OA������O��0��0����A��35��10.5������ֱ��OA����ʽΪs=0.3t��0��t��35��������s=2.1ʱ��0.3t=2.1�����t=7�������˶�Ա�ӵ�һ�ξ���C�㵽�ڶ��ξ���C�����õ�ʱ��Ϊ68���ӣ������˶�Ա����㵽�ڶ��ξ���C�����õ�ʱ����7+68=75���ӣ���ֱ��AB������35��10.5������75��2.1������ֱ��AB����ʽs=kt+b����![]() ����ã�
����ã�![]() ����ֱ��AB ����ʽΪs=��0.21t+17.85��
����ֱ��AB ����ʽΪs=��0.21t+17.85��
�����˶�Ա���������õ�ʱ�伴Ϊֱ��AB��x�ύ��ĺ����꣬����s=0��ʱ����0.21t+17.85=0�����t=85�������˶�Ա����������ʱ85���ӣ�