��Ŀ����
����Ŀ��ijʳƷ���۵�ΪʳƷ������һ�������δ�۳�����������˻س��ң���ͳ������������֣���������������۵���Ϊ7��ʱ��ÿ������160�����ڴ˻����ϣ�����ÿ���1��ʱ�������۵�ÿ��ͻ�������20���������������������۵���Ϊx��(ÿ������ijɱ���5��)�����۵�ÿ�������������������Ϊy�ǣ�
(1)�ú�x�Ĵ���ʽ�ֱ��ʾ��ÿ����������������������������
(2)��x��y֮��ĺ�����ϵʽ��
(3)��������������۵��۶�Ϊ����ʱ�������۵�ÿ���������������õ���������������Ϊ����Ԫ��
���𰸡�
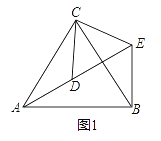
��1�� 
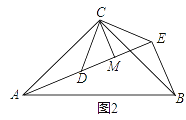
��2�� 
��3�� 
��������
���⣨1����ÿ�����������Ϊ��x��5���ǣ�
��2���������֪y��x�ĺ�����ϵʽ��
��3���Ѻ�����ϵʽ���䷽���ɽ��x=10ʱy�����ֵ��
�⣺��1��ÿ�����������Ϊ��x��5����
�������������Ϊ[160����x��7����20]����4�֣�
��2��y=��300��20x����x��5��=��20x2+400x��1500
��y=��20x2+400x��1500��8�֣�
��3��y=��20x2+400x��1500=��20��x��10��2+500��10�֣�
����x=10ʱ��y�����ֵΪ500��
����ÿ��������۶�Ϊ10��ʱ�������۵�ÿ���õ���������������Ϊ500�ǣ���12�֣�

 ȫ��������ϵ�д�
ȫ��������ϵ�д�