题目内容
【题目】如图，直线y＝ax+b与x轴交于点A（4，0），与y轴交于点B（0，﹣2），与反比例函数y＝
（x＞0）的图象交于点C（6，m）．
（1）求直线和反比例函数的表达式；
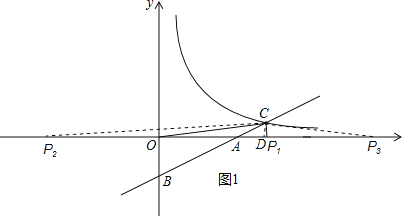
（2）连接OC，在x轴上找一点P，使△OPC是以OC为腰的等腰三角形，请求出点P的坐标；
（3）结合图象，请直接写出不等式≥ax+b的解集．
【答案】（1）y＝
x﹣2；y＝
；（2）点P1的坐标为（
，0），点P2的坐标为（﹣，0），（12，0）；（3）0＜x≤6
【解析】
（1）根据点A，B的坐标，利用待定系数法即可求出直线AB的函数表达式，利用一次函数图象上点的坐标特征可得出点C的坐标，由点C的坐标，利用待定系数法即可求出反比例函数的表达式；
（2）过点C作CD⊥x轴，垂足为D点，利用勾股定理看求出OC的长，分OC＝OP和CO＝CP两种情况考虑：①当OP＝OC时，由OC的长可得出OP的长，进而可求出点P的坐标；②当CO＝CP时，利用等腰三角形的性质可得出OD＝PD，结合OD的长可得出OP的长，进而可得出点P的坐标；
（3）观察图形，由两函数图象的上下位置关系，即可求出不等式
≥ax+b的解集．
解：（1）将A（4，0），B（0，﹣2）代入y＝ax+b，得：
，解得：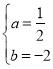
，
∴直线AB的函数表达式为y＝x﹣2．
当x＝6时，y＝x﹣2＝1，
∴点C的坐标为（6，1）．
将C（6，1）代入y＝，得：1＝
，
解得：k＝6，
∴反比例函数的表达式为y＝．
（2）过点C作CD⊥x轴，垂足为D点，则OD＝6，CD＝1，
∴OC＝
．
∵OC为腰，
∴分两种情况考虑，如图1所示：
①当OP＝OC时，∵OC＝，
∴OP＝，
∴点P1的坐标为（，0），点P2的坐标为（﹣，0）；
②当CO＝CP时，DP＝DO＝6，
∴OP＝2OD＝12，
∴点P3的坐标为（12，0）．
（3）观察函数图象，可知：当0＜x＜6时，反比例函数y＝的图象在直线y＝x﹣2的上方，
∴不等式≥ax+b的解集为0＜x≤6．
