题目内容
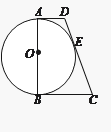
【题目】如图,AB为⊙O的直径,AD与⊙O相切于一点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
⑴求证:BC为⊙O的切线;
⑵若AB=2![]() ,AD=2,求线段BC的长.
,AD=2,求线段BC的长.
【答案】![]()
【解析】
试题(1)因为BC经过圆的半径的外端,只要证明AB⊥BC即可.连接OE、OC,利用△OBC≌△OEC,得到∠OBC=90°即可证明BC为⊙O的切线.
(2)作DF⊥BC于点F,构造Rt△DFC,利用勾股定理解答即可.
试题解析:(1)证明:连接OE、OC.
∵CB=CE,OB=OE,OC=OC,
∴△OBC≌△OEC.
∴∠OBC=∠OEC.
又∵DE与⊙O相切于点E,
∴∠OEC=90°.
∴∠OBC=90°.
∴BC为⊙O的切线.
(2)解:过点D作DF⊥BC于点F,则四边形ABFD是矩形,BF=AD=2,DF=AB=2![]() .
.
∵AD、DC、BC分别切⊙O于点A、E、B,
∴DA=DE,CE=CB.
设BC为x,则CF=x﹣2,DC=x+2.
在Rt△DFC中,(x+2)2﹣(x﹣2)2=(2![]() )2,解得x=
)2,解得x=![]() .
.
∴BC=![]() .
.

练习册系列答案
相关题目
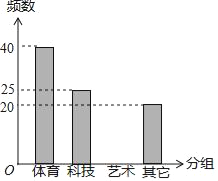
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?