题目内容
【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.

(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
【答案】解:(1)∵四边形ABCD是正方形
∴∠A=∠B=∠D=90°,AD=AB
∵QE⊥AB,MF⊥BC
∴∠AEQ=∠MFB=90°
∴四边形ABFM、AEQD都是矩形
∴MF=AB,QE=AD,MF⊥QE
又∵PQ⊥MN
∴∠EQP=∠FMN
又∵∠QEP=∠MFN=90°
∴△PEQ≌△NFM.
(2)∵点P是边AB的中点,AB=2,DQ=AE=t
∴PA=1,PE=1-t,QE=2
由勾股定理,得PQ=![]() =
=![]()
∵△PEQ≌△NFM
∴MN=PQ=![]()
又∵PQ⊥MN
∴S=![]() =
=![]() =
=![]() t2-t+
t2-t+![]()
∵0≤t≤2
∴当t=1时,S最小值=2.
综上:S=![]() t2-t+
t2-t+![]() ,S的最小值为2.
,S的最小值为2.
【解析】试题分析:(1)由四边形ABCD是正方形得到∠A=∠B=∠D=90°,AD=AB,又由∠EQP=∠FMN,而证得;
(2)分为两种情况:①当E在AP上时,由点P是边AB的中点,AB=2,DQ=AE=t,又由勾股定理求得PQ,由△PEQ≌△NFM得到PQ的值,又PQ⊥MN求得面积S,由t范围得到S的最小值;②当E在BP上时,同法可求S的最小值.
试题解析:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠D=90°,AD=AB,
∵QE⊥AB,MF⊥BC,
∴∠AEQ=∠MFB=90°,
∴四边形ABFM、AEQD都是矩形,
∴MF=AB,QE=AD,MF⊥QE,
又∵PQ⊥MN,
∴∠1+∠EQP=90°,∠2+∠FMN=90°,
∵∠1=∠2,
∴∠EQP=∠FMN,
又∵∠QEP=∠MFN=90°,
∴△PEQ≌△NFM;
(2)分为两种情况:①当E在AP上时,
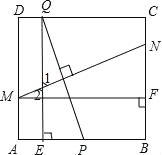
∵点P是边AB的中点,AB=2,DQ=AE=t,
∴PA=1,PE=1-t,QE=2,
由勾股定理,得PQ=![]() ,
,
∵△PEQ≌△NFM,
∴MN=PQ=![]() ,
,
又∵PQ⊥MN,
∴S=![]() t2-t+
t2-t+![]() ,
,
∵0≤t≤2,
∴当t=1时,S最小值=2.
②当E在BP上时,
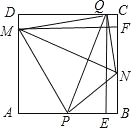
∵点P是边AB的中点,AB=2,DQ=AE=t,
∴PA=1,PE=t-1,QE=2,
由勾股定理,得PQ=![]() ,
,
∵△PEQ≌△NFM,
∴MN=PQ=![]() ,
,
又∵PQ⊥MN,
∴S=![]() t2-t+
t2-t+![]() ,
,
∵0≤t≤2,
∴当t=1时,S最小值=2.
综上:S=![]() t2-t+
t2-t+![]() ,S的最小值为2.
,S的最小值为2.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出80m3的部分 | 2.5 |
超出80m3不超出130m3的部分 | a |
超出130m3的部分 | a+0.5 |
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?