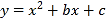��Ŀ����
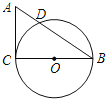
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E��F�ֱ��ڱ�AB��AD�ϣ��ҡ�ECF��45�㣬CF���ӳ��߽�BA���ӳ����ڵ�G��CE���ӳ��߽�DA���ӳ����ڵ�H������AC��EF����GH��
��1����գ���AHC�� ����ACG�������������������
��2���߶�AC��AG��AHʲô��ϵ����˵�����ɣ�
��3����AE��m��
�١�AGH�����S�б仯������仯�������S��m�ĺ�����ϵʽ��������仯���������ֵ��
����ֱ��д��ʹ��CGH�ǵ��������ε�mֵ��

���𰸡���1��=����2�����ۣ�AC2��AGAH�����ɼ���������3���١�AGH��������䣮��m��ֵΪ![]() ��3��12��6
��3��12��6![]() ��.
��.
��������
��1��֤����DAC=��AHC+��ACH=45�㣬��ACH+��ACG=45���������Ƴ���AHC=��ACG��
��2�����ۣ�AC2=AGAH��ֻҪ֤����AHC�ס�ACG���ɽ�����⣻
��3���١�AGH��������䣮���������ε������ʽ���㼴�ɣ�
�ڷ��������ηֱ���⼴�ɽ������.
��1�����ı���ABCD�������Σ�
��AB��CB��CD��DA��4����D����DAB��90����DAC����BAC��45�㣬
��AC��![]() ��
��
�ߡ�DAC����AHC+��ACH��45�㣬��ACH+��ACG��45�㣬
���AHC����ACG��
�ʴ�Ϊ����
��2�����ۣ�AC2��AGAH��
���ɣ��ߡ�AHC����ACG����CAH����CAG��135�㣬
���AHC�ס�ACG��
��![]() ��
��
��AC2��AGAH��
��3���١�AGH��������䣮
���ɣ���S��AGH��![]() AHAG��
AHAG��![]() AC2��
AC2��![]() ����4
����4![]() ��2��16��
��2��16��
���AGH�����Ϊ16��
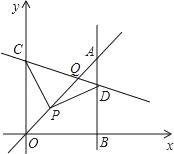
����ͼ1�У���GC��GHʱ����֤��AHG�ա�BGC��
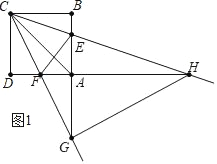
�ɵ�AG��BC��4��AH��BG��8��
��BC��AH��
��![]() ,
,
��AE��![]() AB��
AB��![]() ��
��
��ͼ2�У���CH��HGʱ��
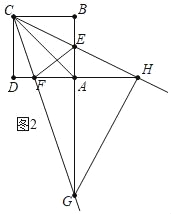
��֤AH��BC��4��
��BC��AH��
��![]() ��1��
��1��
��AE��BE��3��
��ͼ3�У���CG��CHʱ����֤��ECB����DCF��22.5��
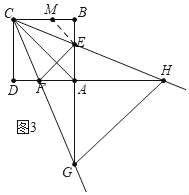
��BC��ȡһ��M��ʹ��BM��BE��
���BME����BEM��45�㣬
�ߡ�BME����MCE+��MEC��
���MCE����MEC��22.5�㣬
��CM��EM����BM��BE��m����CM��EM![]() m��
m��
��m+![]() m��6��
m��6��
��m��6��![]() ��1����
��1����
��AE��6��6��![]() ��1����12��6
��1����12��6![]() ��
��
��������������������m��ֵΪ![]() ��3��12��6
��3��12��6![]() ��
��