题目内容
【题目】如图，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB=13，BC=15，CA=14，则tan∠EDF的值为（ ）
A.
B.
C.
D.
【答案】B
【解析】
由切线长定理可求AF=AE=6，BF=BD=7，CD=CE=8，由勾股定理可得AM=11.2，由三角形面积公式可求EO=4，由圆周角定理可求∠AOE=∠EDF，即可求解．
解：如图，过点A作AM⊥BC，连接AO，BO，CO，EO，FO，DO，
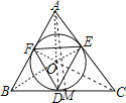
∴EO⊥AC，FO⊥AB，DO⊥BC，OF=OE=OD，
∵△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，
∴AF=AE，BF=BD，CD=CE，
∵AF+BF=AB=13，BD+CD=BC=15，AE+CE=AC=14
∴AF=AE=6，BF=BD=7，CD=CE=8
∵AB2-BM2=AM2，AC2-MC2=AM2，
∴BM=6.6，AM=11.2，
∵S△ABC=S△ABO+S△BCO+S△ACO，
∴
×BC×AM=×AB×FO+×AC×OE+×BC×OD，
∴15×11.2=13EO+14EO+15EO
∴EO=4
∵∠EOF=2∠EDF
∴∠AOE=∠EDF
∴tan∠EDF=tan∠AOE=
=
故选：B．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
