��Ŀ����
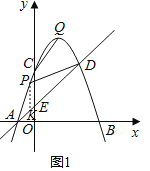
����Ŀ����ͼ��������y��ax2+bx+c��a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C��0��3������OB��OC��3AO��ֱ��y��x+1�������߽���A��D���㣬��y�ύ�ڵ�E����Q�������ߵĶ��㣬��ֱ��AD�Ϸ����������ϵĶ���P�ĺ�����Ϊm��
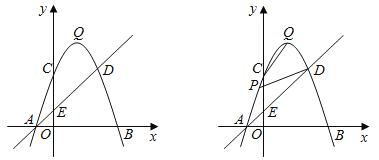
��1����������ߵĽ���ʽ������Q�����ꣻ
��2������CQ���ж��߶�CQ���߶�AE��������ϵ��λ�ù�ϵ����˵�����ɣ�
��3������PA��PD����mΪ��ֵʱ��S��PAD��![]() S��DAB��
S��DAB��
��4����ֱ��AD���Ƿ����һ��Hʹ��PQHΪ����ֱ�������Σ������������m��ֵ����������˵�����ɣ�
���𰸡���1��y����x2+2x+3�� Q��1��4������2���߶�CQ���߶�AE��������ϵ��λ�ù�ϵ��ƽ������ȣ����������������3��m��0��1����4�����ڣ�m��0��2��1![]() ��
��
��������
��1��ֱ��y��x+1�������߽���A�㣬���A����1��0������E��0��1�������B��C������ֱ�Ϊ����3��0������0��3����������⣻
��2��CQ��![]() ��AE��ֱ��AQ��AE����б�Ǿ�Ϊ45����������⣻
��AE��ֱ��AQ��AE����б�Ǿ�Ϊ45����������⣻
��3��S��PAD��![]() ��PK����xD��xA����
��PK����xD��xA����![]() ��3������m2+2m+3��m��1����
��3������m2+2m+3��m��1����![]() S��DAB��
S��DAB��![]() ��4��3��������⣻
��4��3��������⣻
��4���֡�QOH��90������PQH��90������QHP��90������������ֱ���⼴�ɣ�
��1��ֱ��y��x+1�������߽���A�㣬���A����1��0������E��0��1����
���B��C������ֱ�Ϊ����3��0������0��3����
�������ߵı���ʽΪ��y��a��x+1����x��3����a��x2��2x��3����
����3a��3����ã�a����1��
�������ߵı���ʽΪ��y����x2+2x+3��
�����ĶԳ���Ϊ��x��1���ʵ�Q��1��4����
��2��CQ��![]() ��AE��ֱ��AQ��AE����б�Ǿ�Ϊ45����
��AE��ֱ��AQ��AE����б�Ǿ�Ϊ45����
���߶�CQ���߶�AE��������ϵ��λ�ù�ϵ��ƽ������ȣ�
��3������ֱ��y��x+1�������ߵı���ʽ����ã�x��0��2���ʵ�D��2��3����
����P��y���ƽ���߽�AD�ڵ�K��
���P��m����m2+2m+3�������K��m��m+1����
S��PAD��![]() ��PK����xD��xA����
��PK����xD��xA����![]() ��3������m2+2m+3��m��1����
��3������m2+2m+3��m��1����![]() S��DAB��
S��DAB��![]() ��4��3��
��4��3��
��ã�m��0��1��
�ʵ�P��0��3����1��4����
��4�����ڣ����ɣ�
���H��t��t+1������P��m��n����n����m2+2m+3������Q��1��4����
�ٵ���QOH��90��ʱ����ͼ1��
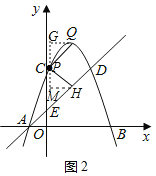
����O��y���ƽ���ߣ��ֱ���H����Q��x���ƽ�����ڵ�M��G��
�ߡ�GQP+��QPG��90������QPG+��HPM��90�������HPM����GQP��
��PGQ����HMP��90����PH��PQ��
���PGQ�ա�HMP��AAS������PG��MH��GQ��PM��
����4��n��t��m��1��m��n��t��1��
��ã�m��0��2��
�ʵ�P��2��3����0��3����
�ڵ���PQH��90��ʱ��
���QHP����QPH��45������PH��x�ᣬ
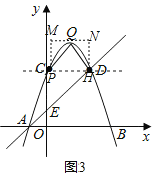
ͬ���ɵã�m��0��2��
�ʵ�P��2��3����0��3����
�۵���QHP��90��ʱ��
����H�ڵ�D���·�ʱ�������ͼ��
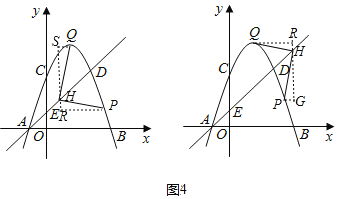
ͬ���ɵã�m��3��
�ʵ�P��3��0����
����H�ڵ�D���·�ʱ�����Ҳ�ͼ��
ͬ���ɵã�m��1![]() ��
��
�ʵ�P��1+![]() ��2����1��
��2����1��![]() ��2����
��2����
���ϣ���P������Ϊ����2��3����0��3����3��0����1+![]() ��2����1��
��2����1��![]() ��2����
��2����