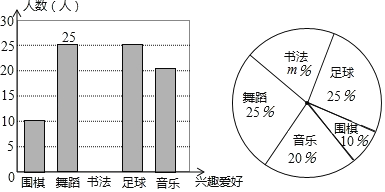
题目内容
【题目】童老师计划购买A、B两种笔记本共30本作为班会奖品,这两种笔记本的单价分别是12元和8元,并且购买的A种笔记本的数量要少于B种笔记本数量的![]() ,但又不少于B种笔记本数量的
,但又不少于B种笔记本数量的![]() .如果设买A种笔记本x本,买这两种笔记本共花费y元.
.如果设买A种笔记本x本,买这两种笔记本共花费y元.
(1)求计划购买这两种笔记本所需的费用y(元)关于x(本)的函数关系式;
(2)童老师有多少种不同的购买方案?
(3)商店为了促销,决定对A种笔记本每本让利a(4<a≤7)元销售,B种笔记本每本让利b元销售,童老师发现购买所需的总费用与购买的方案无关.当总费用最少时,求此时a、b的值.
【答案】(1)y=4x+240;(2)7种不同的购买方案;(3)当总费用最少时,a、b的值分别为7,3.
【解析】
(1)根据题意可以得到y与x的函数关系式,本题得以解决;
(2)根据题意可以列出相应的不等式,从而可以求得购买方案;
(3)根据题意,可以列出y与x的函数关系式,再根据童老师发现购买所需的总费用与购买的方案无关,4<a≤7,可以求得当总费用最少时,a、b的值.
解:(1)由题意可得,
y=12x+8(30-x)=4x+240,
即计划购买这两种笔记本所需的费用y(元)关于x(本)的函数关系式是y=4x+240;
(2)∵购买的A种笔记本的数量要少于B种笔记本数量的![]() ,但又不少于B种笔记本数量的
,但又不少于B种笔记本数量的![]() ,
,
∴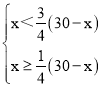 ,得6≤x<12
,得6≤x<12![]() ,
,
∵x为整数,
∴共有12-6+1=7种不同的购买方案;
(3)由题意可得,
y=(12-a)x+(8-b)(30-x)=(4-a+b)x+240-30b,
∵童老师发现购买所需的总费用与购买的方案无关,
∴4-a+b=0,
∴a=4+b,
∵4<a≤7,
∴4<4+b≤7,
∴0<b≤3,
∴y=240-30b,
∴当b=3时,y取得最小值,此时y=150,a=4+b=7,
答:当总费用最少时,a、b的值分别为7,3.

 通城学典默写能手系列答案
通城学典默写能手系列答案