题目内容
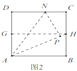
【题目】如图1,在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于
轴于![]() ,
,![]() 两点.点
两点.点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点.
两点.
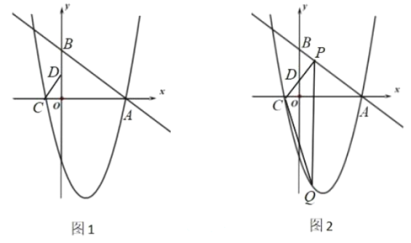
(1)求抛物线的表达式;
(2)如图1,![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,若
,若![]() 的值最小,求
的值最小,求![]() 点坐标;
点坐标;
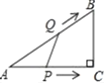
(3)如图2,在(2)的前提下,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,过
,过![]() 点作
点作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,若
,若![]() 是抛物线上一点,
是抛物线上一点,![]() 是
是![]() 轴上一点,是否存在以
轴上一点,是否存在以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点且
为顶点且![]() 为边的平行四边形,若存在,求出
为边的平行四边形,若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)D点坐标为(0,
;(2)D点坐标为(0,![]() );(3)存在,点M的坐标为(
);(3)存在,点M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)先求得点A的坐标,再将A、C的坐标代入抛物线的表达式即可求解;
(2)过点D作DG⊥AB于G,利用∠OBA的正弦值求得DG=![]() BD,则C、D、G三点共线时,CD+
BD,则C、D、G三点共线时,CD+![]() BD的值最小,即可求得D点坐标;
BD的值最小,即可求得D点坐标;
(3)先求得Q点坐标,分CQ为对角线、CM为对角线、CN为对角线三种情况讨论即可求解.
(1)令![]() ,则
,则![]() ,
,
解得:![]() ,
,
∴点A的坐标为(4,0),
∵抛物线![]() 经过
经过![]() ,
,![]() 两点,
两点,
∴将A(4,0)、C(-1,0)的坐标代入得:
![]() ,
,
解得:![]() ,
,
∴抛物线的表达式为:![]() ;
;
(2)令![]() ,则
,则![]() ,
,
∴点B的坐标为(0,3),
∴OA=4,OB=3,
∴![]() ,
,
过点D作DG⊥AB于G,如图:
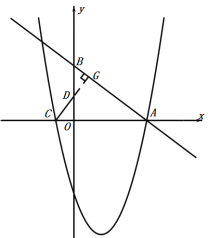
∵![]() ,
,
∴DG=![]() BD,
BD,
当C、D、G三点共线时,CD+![]() BD的值最小,
BD的值最小,
∵点C的坐标为(-1,0),
∴OC=1,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴D点坐标为(0,![]() );
);
(3)设直线CD的解析式为:![]() ,
,
将点C(-1,0)的坐标代入得:![]() ,
,
解得:![]() ,
,
∴直线CD的解析式为:![]() ,
,
解方程组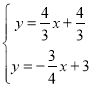 得:
得: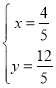 ,
,
∴P点坐标为(![]() ,
,![]() );
);
∵PQ∥y轴,
当![]() 时,
时,![]() ,
,
∴Q点坐标为(![]() ,
,![]() );
);
当CQ为对角线时,C、Q中点与M、N中点相同,
设M点的横坐标为![]() ,
,
则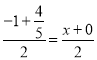 ,
,
解得:![]() ,
,
当![]() 时,
时,![]() ,
,
∴M点坐标为(![]() ,
,![]() );
);
当CM为对角线时,C、M中点与Q、N中点相同,
设M点的横坐标为![]() ,
,
则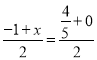 ,
,
解得:![]() ,
,
当![]() 时,
时,![]() ,
,
∴M点坐标为(![]() ,
,![]() );
);
当CN为对角线时,C、N中点与M、Q中点相同,
设M点的横坐标为![]() ,
,
则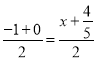 ,
,
解得:![]() ,
,
当![]() 时,
时,![]() ,
,
∴M点坐标为(![]() ,
,![]() );
);
综上可知,点M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)

 名校课堂系列答案
名校课堂系列答案